import numpy as np
import matplotlib.pyplot as plt
import sklearn
from sklearn.datasets import load_digits
from sklearn.decomposition import TruncatedSVD
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.ensemble import RandomTreesEmbedding
from sklearn.manifold import (Isomap, LocallyLinearEmbedding, MDS, SpectralEmbedding, TSNE)
from sklearn.neighbors import NeighborhoodComponentsAnalysis
from sklearn.pipeline import make_pipeline
from sklearn.random_projection import SparseRandomProjection
from sklearn.decomposition import PCA
import plotly.graph_objects as go
from umap import UMAPWelcome back to the Visualization for Machine Learning Lab!
Week 7: Clustering and Dimensionality Reduction
Miscellaneous
- Homework 3 has been posted and is due next Friday (3/15) at 11:59pm
- Homework 2 is being graded, grades will likely be posted next week
Dimensionality Reduction
- Various methods of projecting data into a low-dimensional space while preserving the clusters from the high-dimensional space
- Principal Component Analysis (PCA)
- Multidimensional Scaling (MDS)
- Sparse Random Projection
- Locally Linear Embedding
- Uniform Manifold Approximation and Projection (UMAP)
- t-Distributed Stochastic Neighbor Embedding (t-SNE)
MNIST Dataset
- Dataset of 28x28 pixel images of handwritten digits
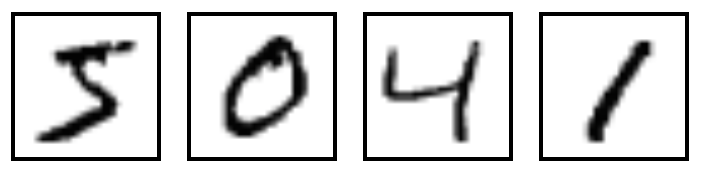
Ref: Olah (2014)
MNIST Dataset
- Every MNIST image can be thought of as a 28x28 array of numbers describing how dark each pixel is:
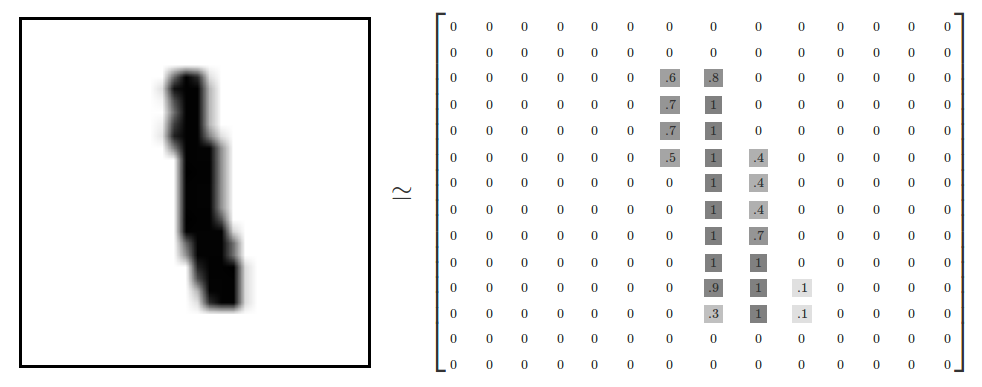
- We can flatten each array into a 28 * 28 = 784 dimensional vector, where each component of the vector is a value between zero and one describing the intensity of the pixel
- We can think of MNIST as a collection of 784-dimensional vectors
Ref: Olah (2014)
MNIST Dataset
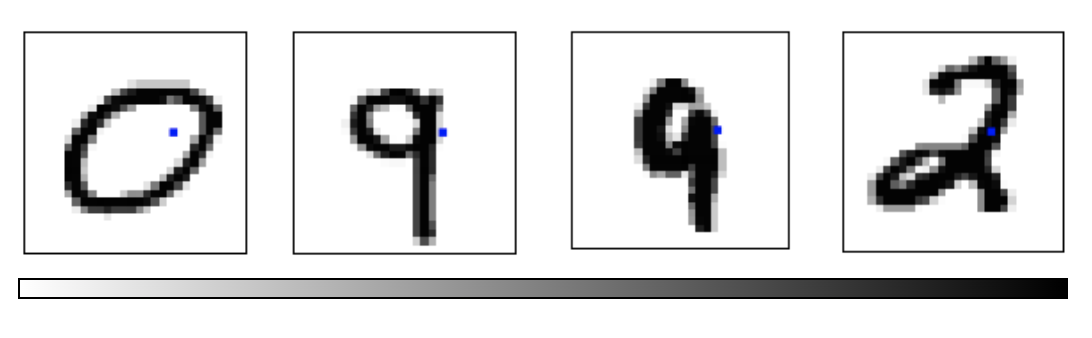
- But not all vectors in this 784-dimensional space are MNIST digits! Typical points in this space are very different
- To get a sense of what a typical point looks like, we can randomly pick a few random 28x28 images – each pixel is randomly black, white or some shade of gray. These random points look like noise:

Ref: Olah (2014)
MNIST Dataset
- 28x28 images that look like MNIST digits are very rare - they make up a very small subspace of 784-dimensional space
- With some slightly harder arguments, we can see that they occupy a lower (than 748) dimensional subspace
- Many theories about lower-dimensional structure of MNIST (and similar data)
- Manifold hypothesis (popular among ML researchers): MNIST is a low dimensional manifold curving through its high-dimensional embedding space
- Another hypothesis (rooted in topological data analysis) is that data like MNIST consists of blobs with tentacle-like protrusions sticking out into the surrounding space
- But no one actually knows for sure!
Ref: Olah (2014)
MNIST Cube
- Imagine the MNIST data points as points suspended in a 784-dimensional cube
- Each dimension of the cube corresponds to a particular pixel
- The data points range from zero to one according to pixel intensity
- On one side of the dimension, there are images where that pixel is white. On the other side of the dimension, there are images where it is black. In between, there are images where it is gray.
- What does this cube look like if we look at a particular two-dimensional face? Let's look at @Olah_2014's visualizations.
Ref: Olah (2014)
MNIST Cube
- What qualities would the ‘perfect’ visualization of MNIST have? What should our goal be?
- What is the best way to cluster MNIST data?
- We can try what we learned last week…
Ref: Olah (2014)
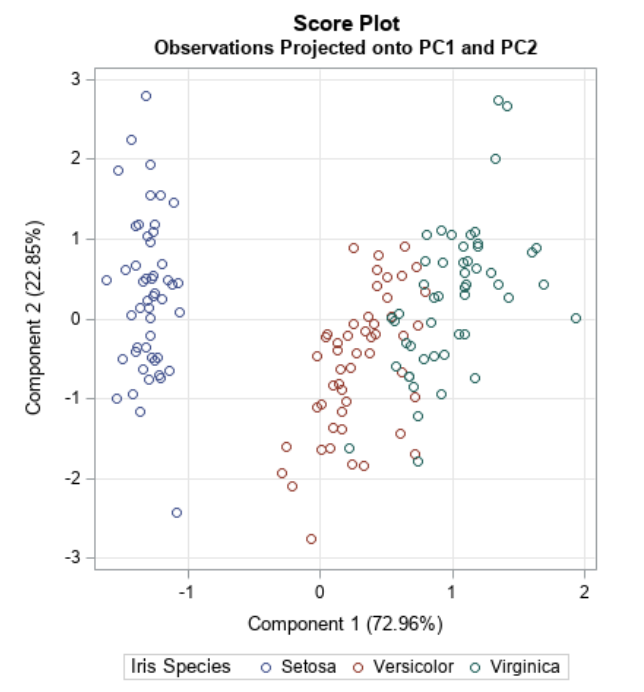
Principal Component Analysis Recap
- Dimensionality reduction technique that allows us to find clusters of similar data points based on many features (which we boil down to two “principal components” PC1 and PC2)
- PC1 and PC2 represent the directions in the data space with the highest and second-highest variances, respectively
- Way to bring out strong patterns from large and complex datasets
Ref: Team (2018)
PCA on MNIST
Import libraries:
PCA on MNIST
Define helper functions for visualizing clusters in 2D and 3D:
# Authors: Gael Varoquaux
# License: BSD 3 clause (C) INRIA 2014
def plot_clustering(X_red, labels, title=None):
x_min, x_max = np.min(X_red, axis=0), np.max(X_red, axis=0)
X_red = (X_red - x_min) / (x_max - x_min)
plt.figure(figsize=(6, 6))
for digit in digits.target_names:
plt.scatter(
*X_red[y == digit].T,
marker=f"${digit}$",
s=50,
# c=plt.cm.nipy_spectral(labels[y == digit] / 10),
alpha=0.5,
)
plt.xticks([])
plt.yticks([])
if title is not None:
plt.title(title, size=17)
plt.axis("off")
plt.tight_layout(rect=[0, 0.03, 1, 0.95])PCA on MNIST
Define helper functions for visualizing clusters in 2D and 3D:
def plot_3d_clustering(X_red, labels, title=None):
component0 = X_red[:, 0]
component1 = X_red[:, 1]
component2 = X_red[:, 2]
indices = list(range(X_red.shape[0]))
labels = list (map(lambda x: "label:" + str(y[x]) + ", id:" + str(x),indices))
fig = go.Figure(data=[go.Scatter3d(
x=component0,
y=component1,
z=component2,
mode='markers',
marker=dict(
size=10,
color=y, # set color to an array/list of desired values
colorscale='Rainbow', # choose a colorscale
opacity=1,
line_width=1,
),
text = labels
)])
# tight layout
fig.update_layout(margin=dict(l=50,r=50,b=50,t=50),width=520,height=520)
fig.layout.template = 'plotly_dark'
fig.show()PCA on MNIST
Load the MNIST dataset:
PCA on MNIST
Peform PCA:
PCA on MNIST
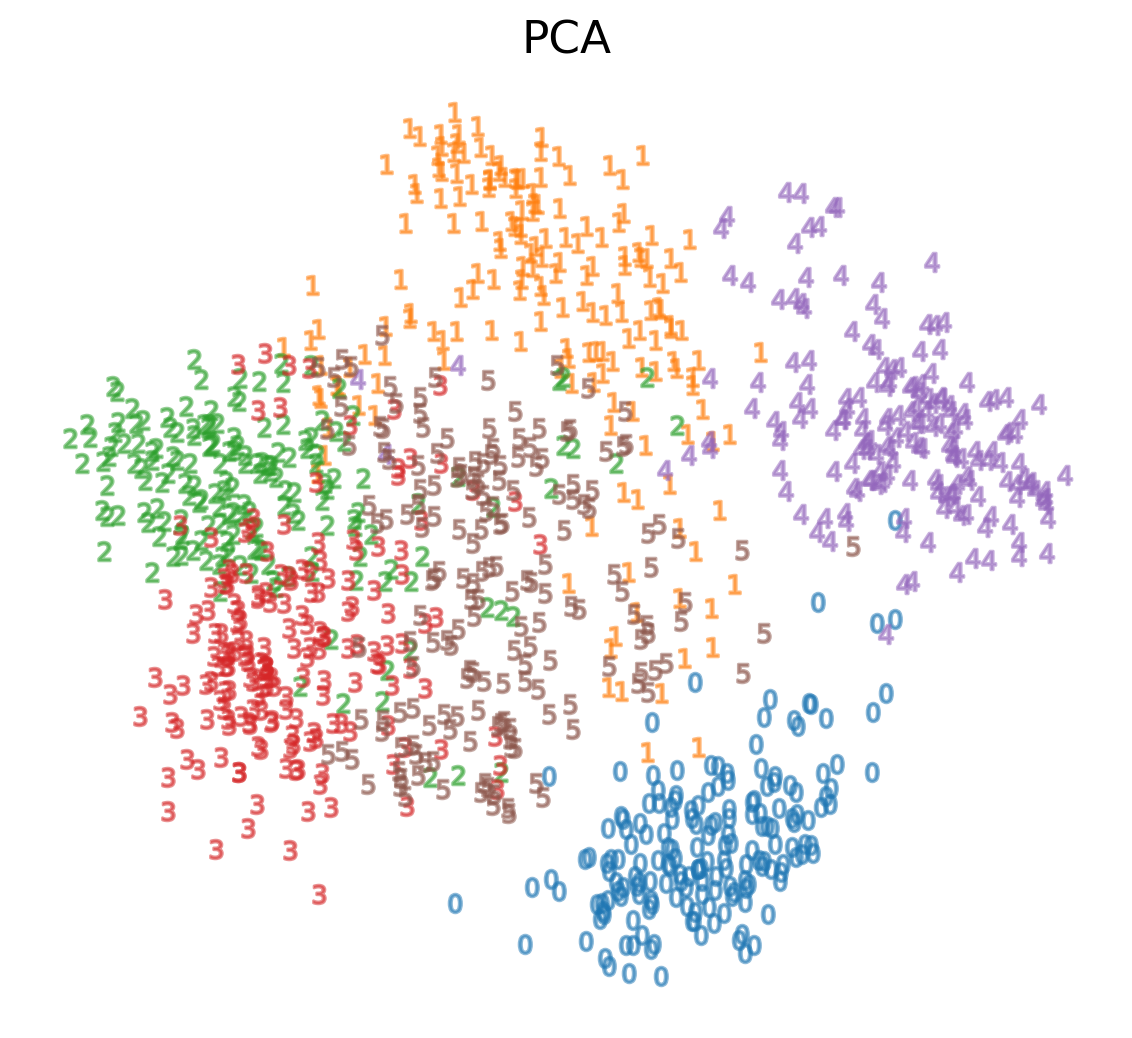
-
We see that we are able to reasonbly cluster the data by digit using PCA:
PCA on MNIST
-
We see that we are able to reasonbly cluster the data by digit using PCA:
PCA on MNIST
-
We can also visualize this in 3D:
Optimization-Based Dimensionality Reduction
- What if the distances between points in our visualization were the same as the distances between points in the original space?
- This captures the global geometry of the data
- In this case, we say that for any two MNIST data points, xi and xj, there are two notions of distance between them:
- d*i,j denotes the distance between xi and xj in the original space
- di,j denotes the distance between xi and xj in our visualization.
- Now we can define a cost:
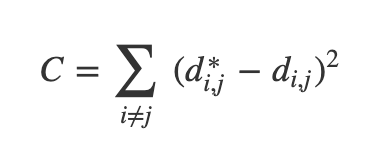
Ref: Olah (2014)
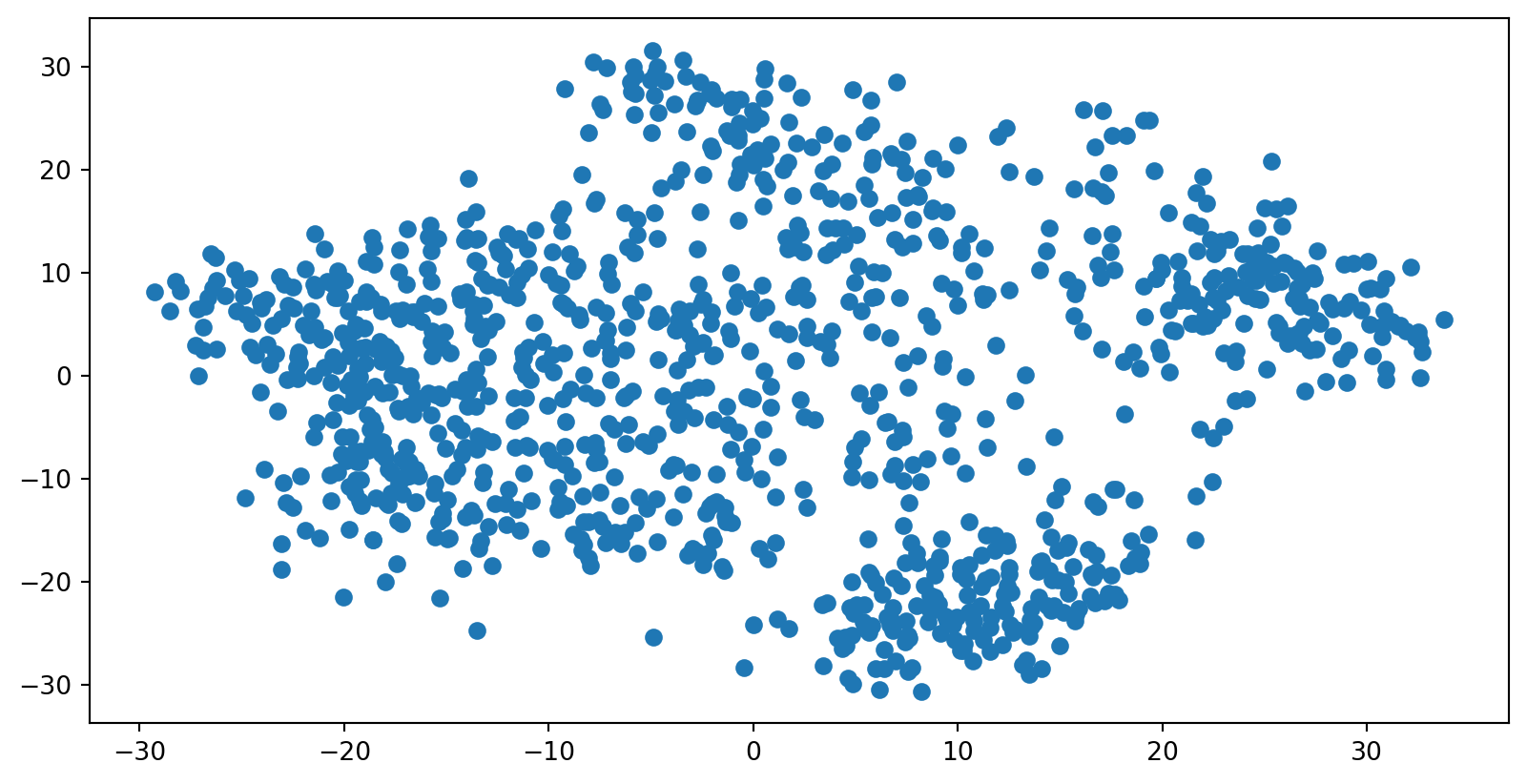
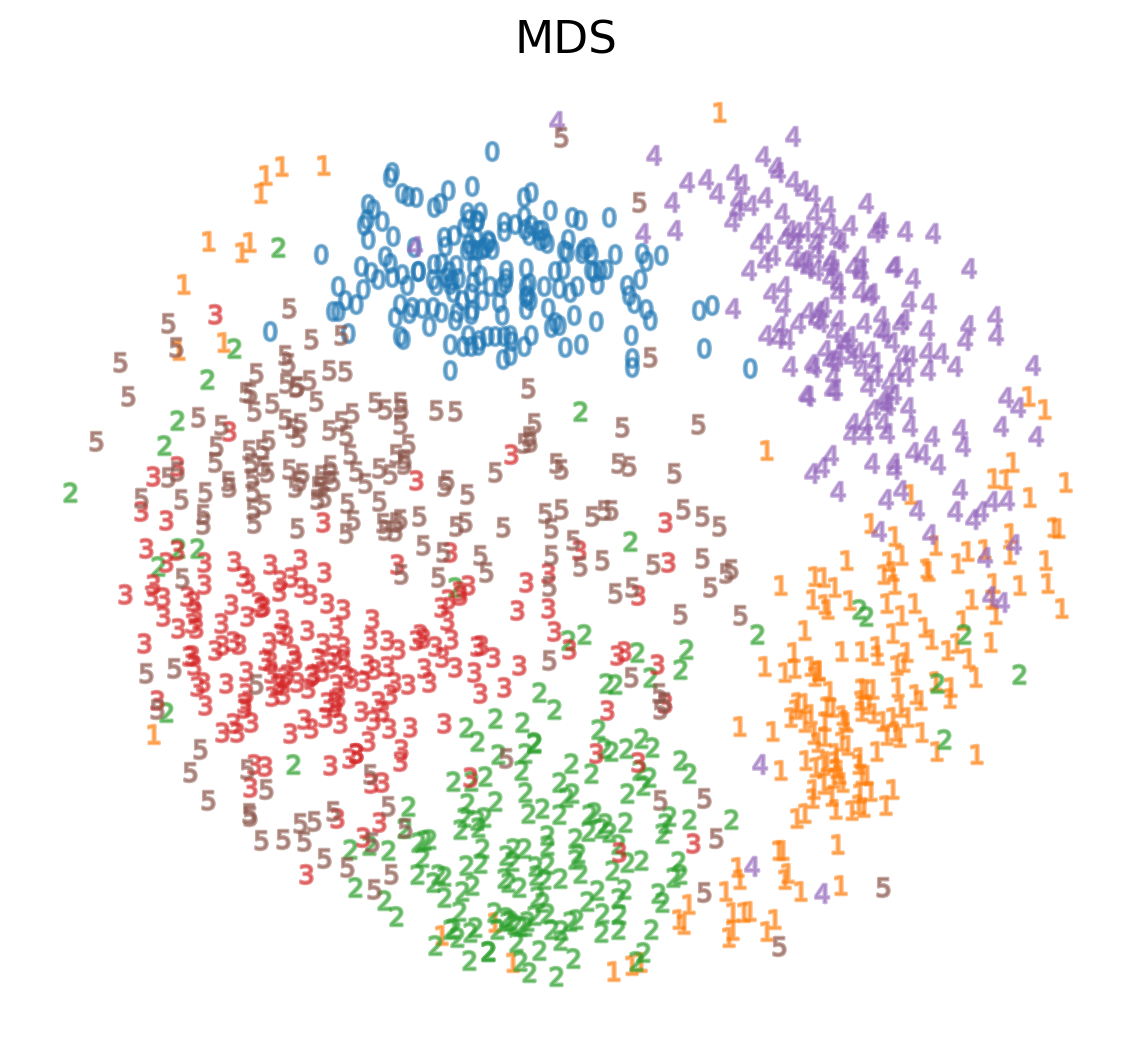
Multidimensional Scaling (MDS)
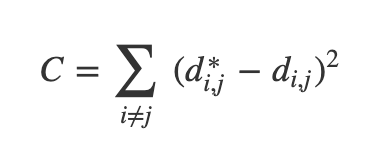
- If these distances are similar, the cost is low (and vice versa). So a cost of zero is optimal (though we can never actually reach this)
- We can solve this as an optimization problem - we start with a random point and apply gradient descent
- This is called multidimensional scaling (MDS)
Ref: Olah (2014)
MDS on MNIST
MDS on MNIST
Sammon’s Mapping
- There are many variations of MDS
- Common theme is to use a cost function that emphasizes local structure as more important to maintain than global structure
- One version of this is Sammon's Mapping, which uses the cost function:
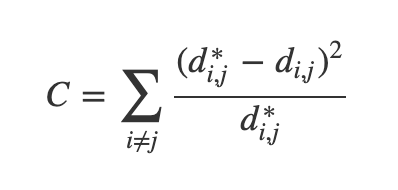
- In Sammon’s mapping, we try harder to preserve the distances between nearby points than between those which are far apart. If two points are twice as close in the original space as two others, it is twice as important to maintain the distance between them.
Ref: Olah (2014)
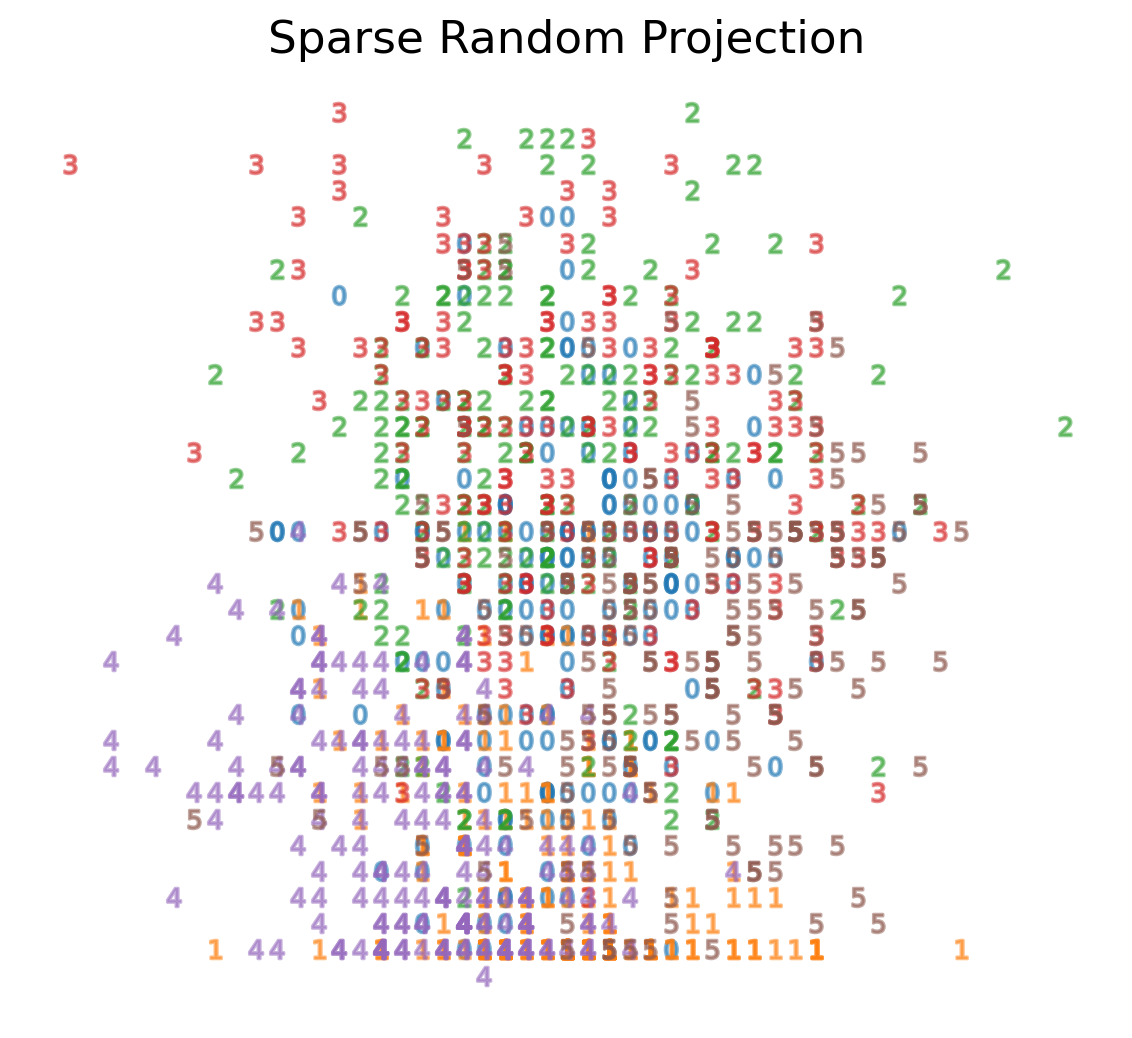
Sparse Random Projection
- Reduces the dimensionality by projecting the original input space using a sparse random matrix
- Alternative to dense Gaussian random projection matrix - guarantees similar embedding quality while being much more memory efficient and allowing faster computation of the projected data
- If we define s = 1 / density, the elements of the random matrix are drawn from

-
where ncomponents is the size of the projected subspace. <li style=“font-size:30px”;>By default the density of nonzero elements is set to the minimum density as recommended by Ping Li et al: 1 /
Ref: (n.d.)
Sparse Random Projection on MNIST
Sparse Random Projection on MNIST
Locally Linear Embedding
- First we find the k-nearest neighbors of each data point
- One advantage of the LLE algorithm is that there is only one parameter to tune (K). If K is chosen to be too small or too large, it will not be able to accomodate the geometry of the original data. Here, for each data point that we have we compute the K nearest neighbours.
- Next, we approximate each data vector as a weighted linear combination of its k-nearest neighbors to construct new points. We try to minimize the cost function, where j’th nearest neighbour for point Xi.
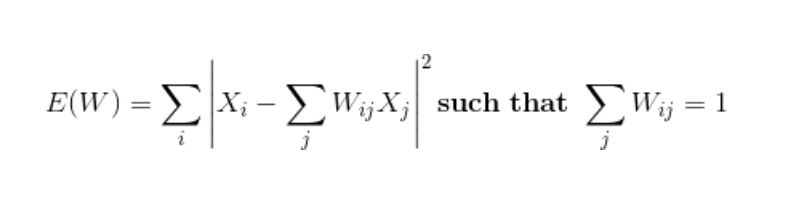
Ref: Mihir (2024)
Locally Linear Embedding
- Finally, it computes the weights that best reconstruct the vectors from its neighbors, then produce the low-dimensional vectors best reconstructed by these weights.
- In other words, we define the new vector space Y such that we minimize the cost for Y as the new points:
Ref: Mihir (2024)
Locally Linear Embedding
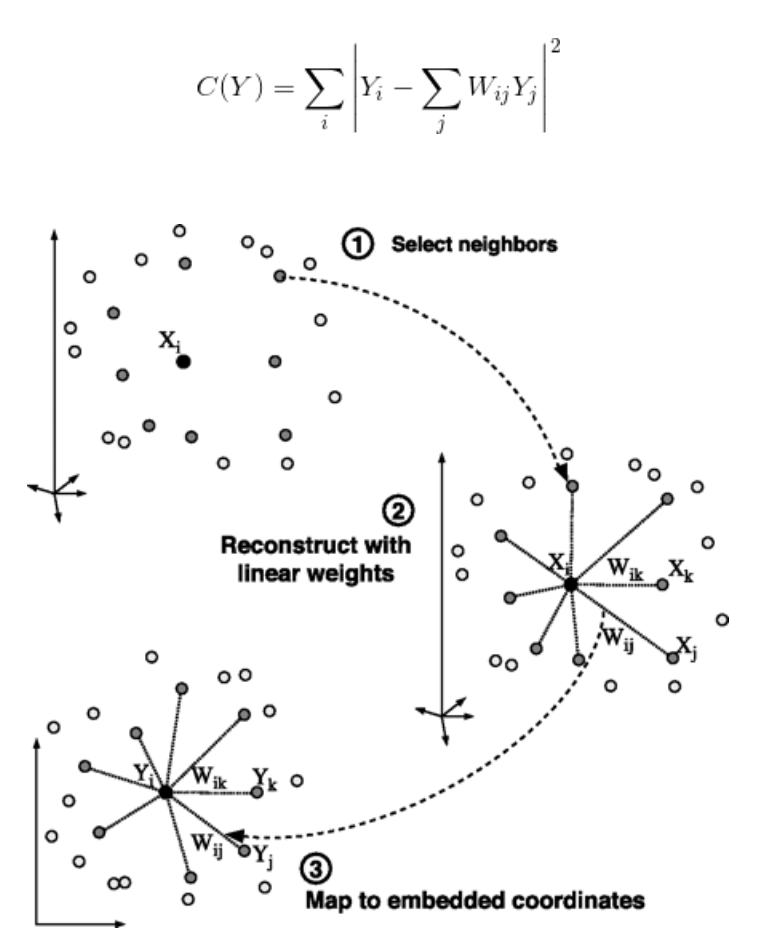
Ref: Mihir (2024)
LLE on MNIST
LLE on MNIST
t-Distributed Stochastic Neighbor Embedding (t-SNE)
- Very popular for deep learning
- Tries to optimize for preserving the topology of the data
- For every point, t-SNE constructs a notion of which other points are its ‘neighbors,’ trying to make all points have the same number of neighbors. Then it tries to embed them so that those points all have the same number of neighbors.
Ref: Olah (2014)
t-SNE
Ref: Starmer (2017)
t-SNE on MNIST
t-SNE on MNIST
Using t-SNE Effectively
- t-SNE plots are popular and can be useful, but only if you avoid common misreadings
- Beware of hyperparameter values
- Remember cluster sizes in a t-SNE plot mean nothing
- Know that distances BETWEEN clusters may not mean anything either
- Random noise doesn’t always look random
- You may need multiple plots for topology
- See Wattenberg, Viégas, and Johnson (2016) for more details
Ref: Wattenberg, Viégas, and Johnson (2016)
Uniform Manifold Approximation and Projection (UMAP)
- Similar to t-SNE, but with some advantages:
- Increased speed
- Better preservation of the data’s global structure
Ref: Coenen and Pearce (n.d.)
Uniform Manifold Approximation and Projection (UMAP)
- UMAP constructs a high dimensional graph representation of the data then optimizes a low-dimensional graph to be as structurally similar as possible
- Starts with "fuzzy simplicial complex," a representation of a weighted graph with edge weights representing the likelihood that two points are connected.
- To determine connectedness, UMAP extends a radius outwards from each point, connecting points when those radii overlap.
- Choice of radius matters! Too small = small, isolated clusters. Too large = everything is connected. UMAP overcomes this challenge by choosing a radius locally, based on the distance to each point's nth nearest neighbor.
- The graph is made "fuzzy" by decreasing the likelihood of connection as the radius grows
- By stipulating that each point must be connected to at least its closest neighbor, UMAP ensures that local structure is preserved in balance with global structure
Ref: Coenen and Pearce (n.d.)
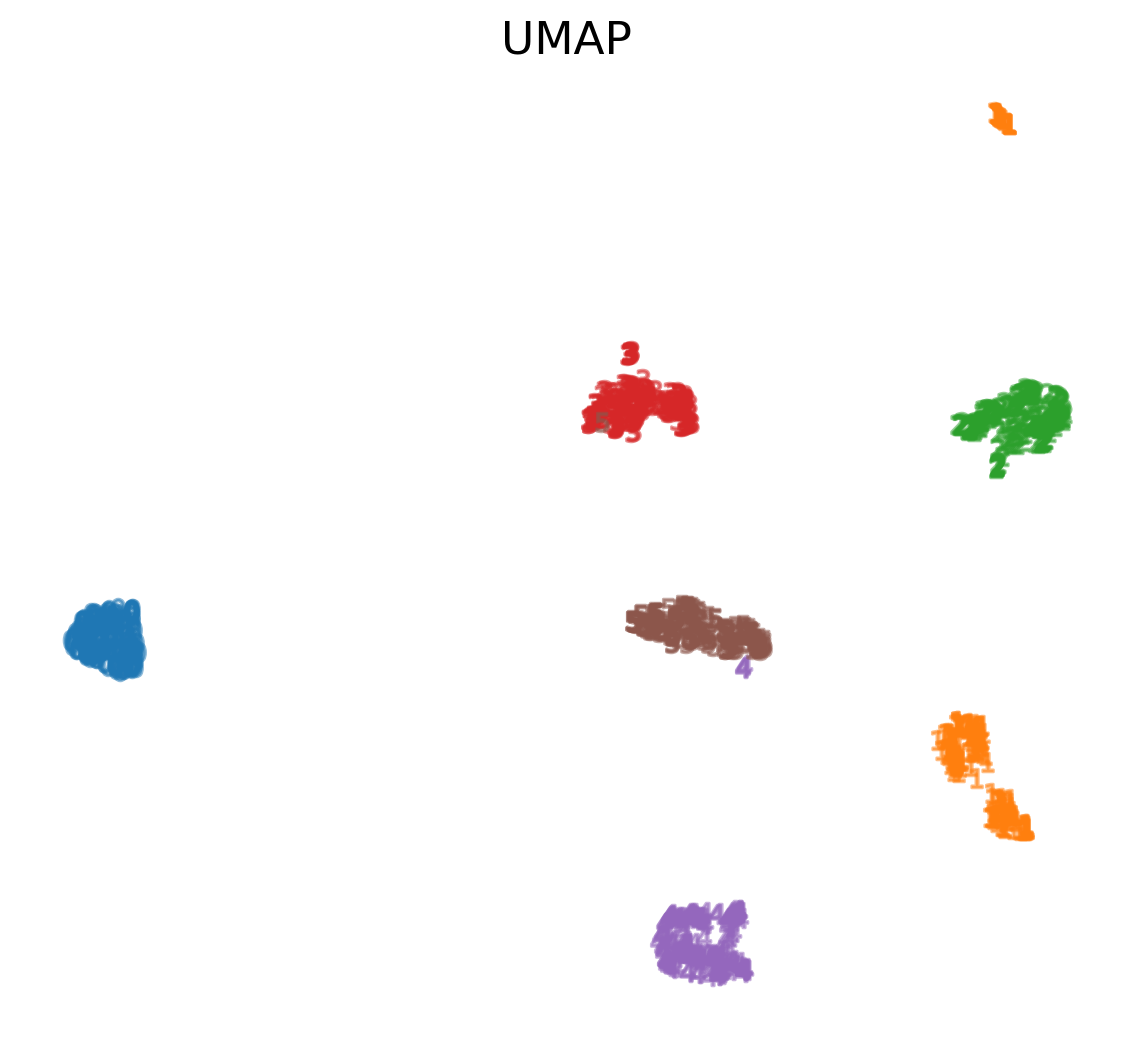
UMAP on MNIST
References (Good for Further Reading)
Coenen, Andy, and Adam Pearce. n.d. “Understanding Umap.” Understanding UMAP. Google PAIR. https://pair-code.github.io/understanding-umap/.
Mihir. 2024. “Locally Linear Embedding (LLE): Data Mining.” Medium. Analytics Vidhya. https://medium.com/analytics-vidhya/locally-linear-embedding-lle-data-mining-b956616d24e9.
Olah, Christopher. 2014. “Visualizing Mnist: An Exploration of Dimensionality Reduction.” Visualizing MNIST: An Exploration of Dimensionality Reduction - Colah’s Blog. https://colah.github.io/posts/2014-10-Visualizing-MNIST/.
Starmer, Josh. 2017. “StatQuest: T-Sne, Clearly Explained.” YouTube. YouTube. https://www.youtube.com/watch?v=NEaUSP4YerM&ab_channel=StatQuestwithJoshStarmer.
Team, BioTuring. 2018. “Principal Component Analysis Explained Simply.” Medium. Medium. https://bioturing.medium.com/principal-component-analysis-explained-simply-894e8f6f4bfb.
Wattenberg, Martin, Fernanda Viégas, and Ian Johnson. 2016. “How to Use t-Sne Effectively.” Distill. https://distill.pub/2016/misread-tsne/.