Welcome back to the Visualization for Machine Learning Lab!
Week 9: Topological Data Analysis
Miscellaneous
- Homework 4 (on dimensionality reduction) will be released next week. It will NOT be mandatory - complete it by April 19th for extra credit
- Homework 3 is being graded
- Project proposal due 4/4 - please submit the names of your project team here by the end of today! Only one person from each team needs to complete the form.
- I will be holding office hours at 2pm Tuesday and Thursday next week - reach out if you want to discuss your proposal and neither time works for you
Topological Data Analysis (TDA)
- Data has shape, and that shape matters when we analyze it
- A way of extracting meaning from high dimensional data
- Slides adapted from Shaw Talebi’s TDA video trilogy.
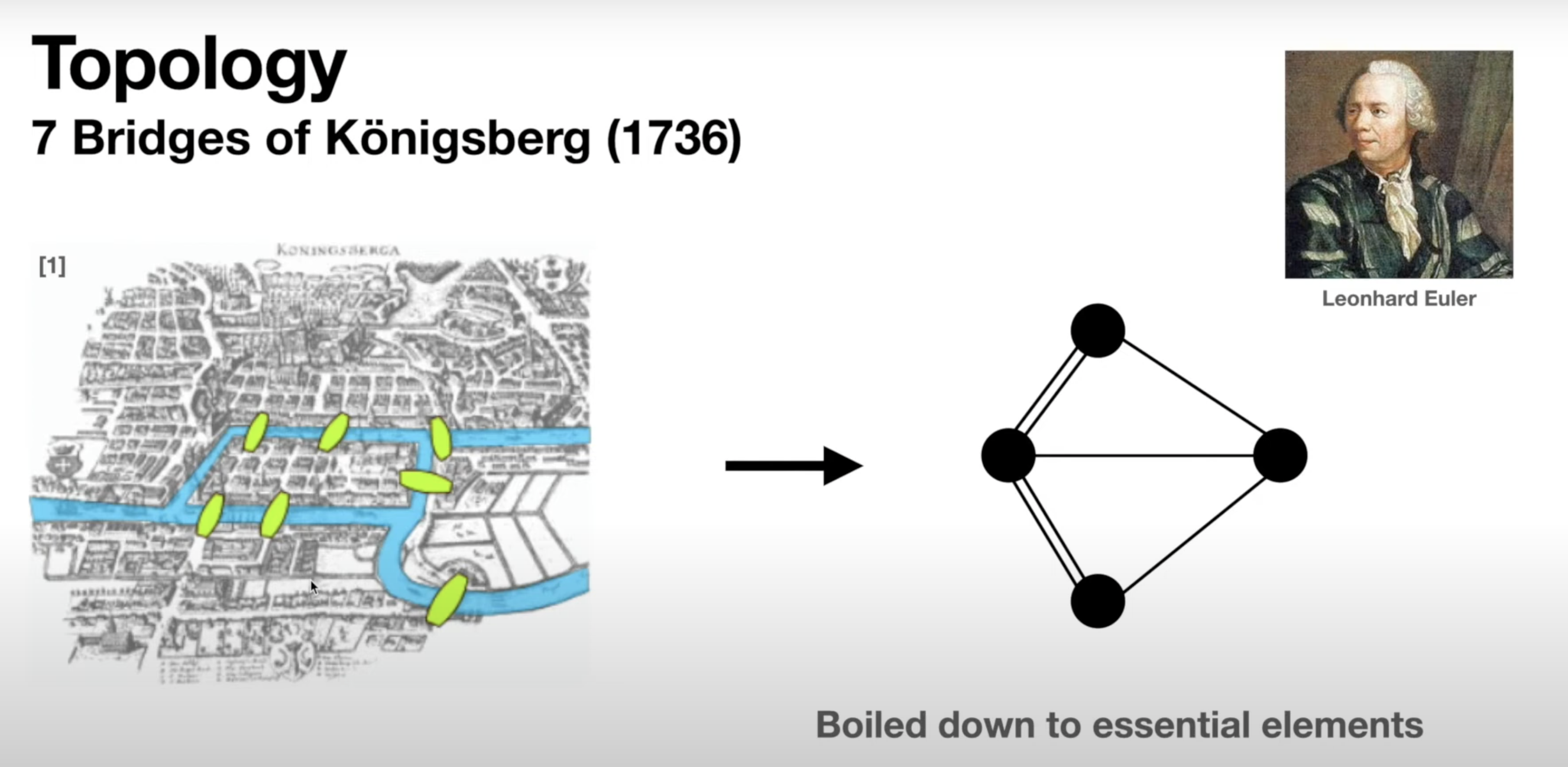
The Seven Bridges of Königsberg
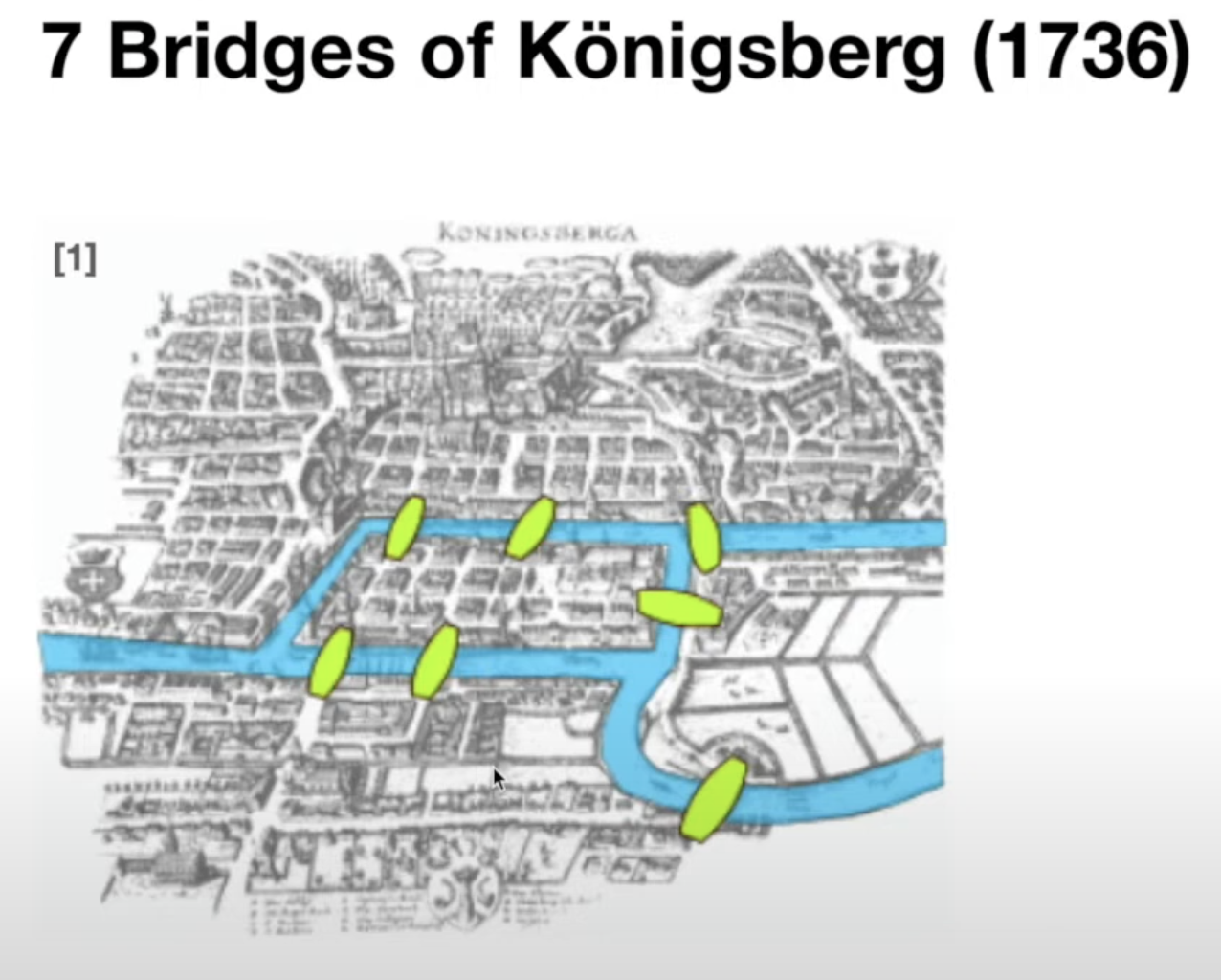
The Seven Bridges of Königsberg
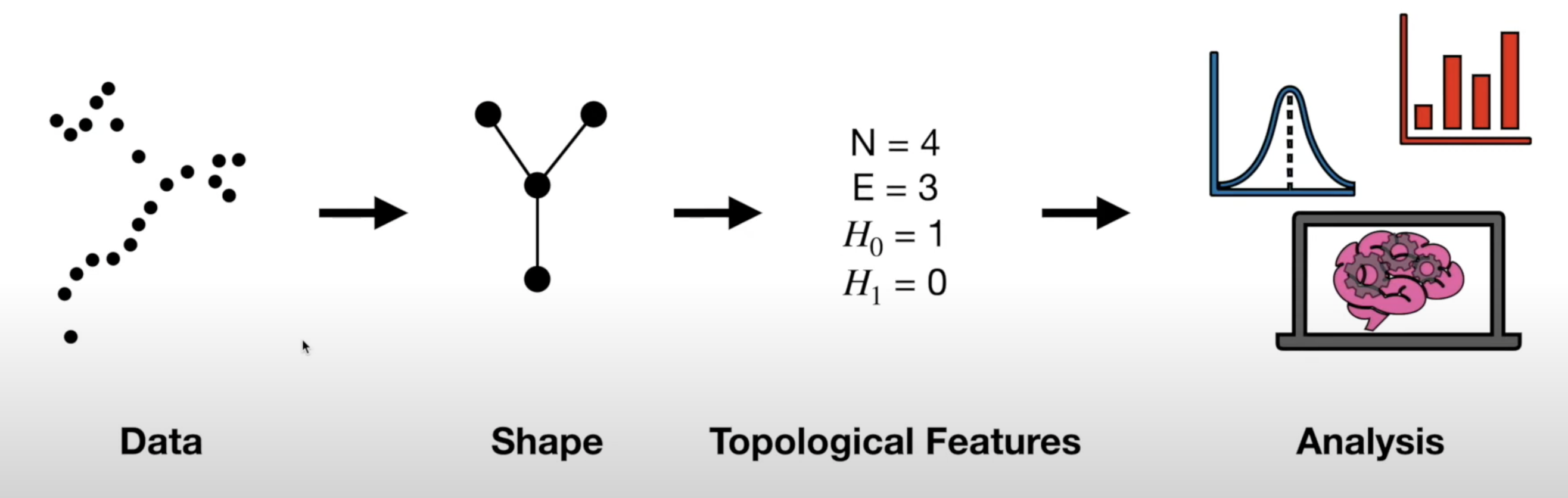
General TDA Pipeline
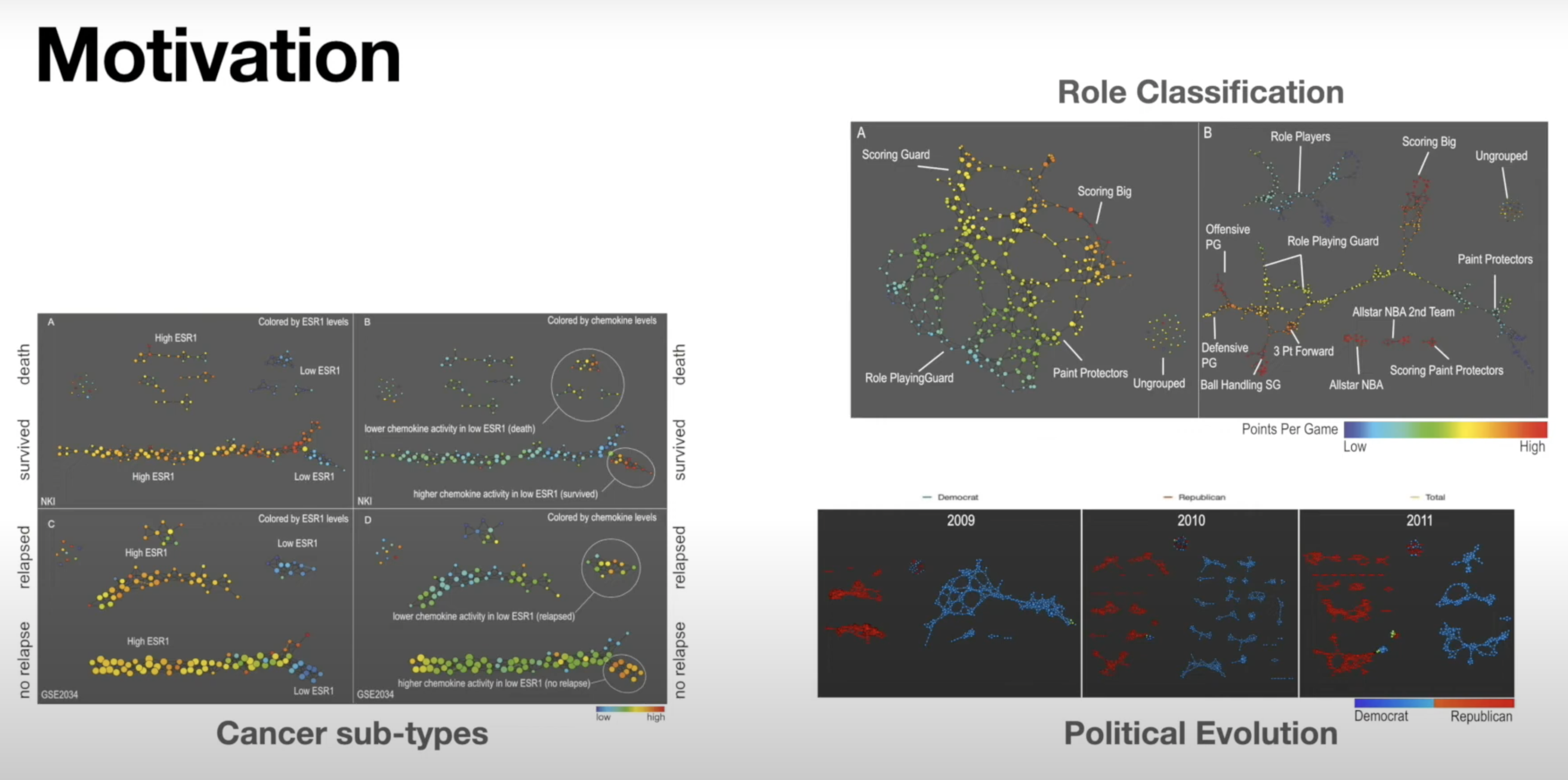
Real World Applications of TDA
Mapper Algorithm
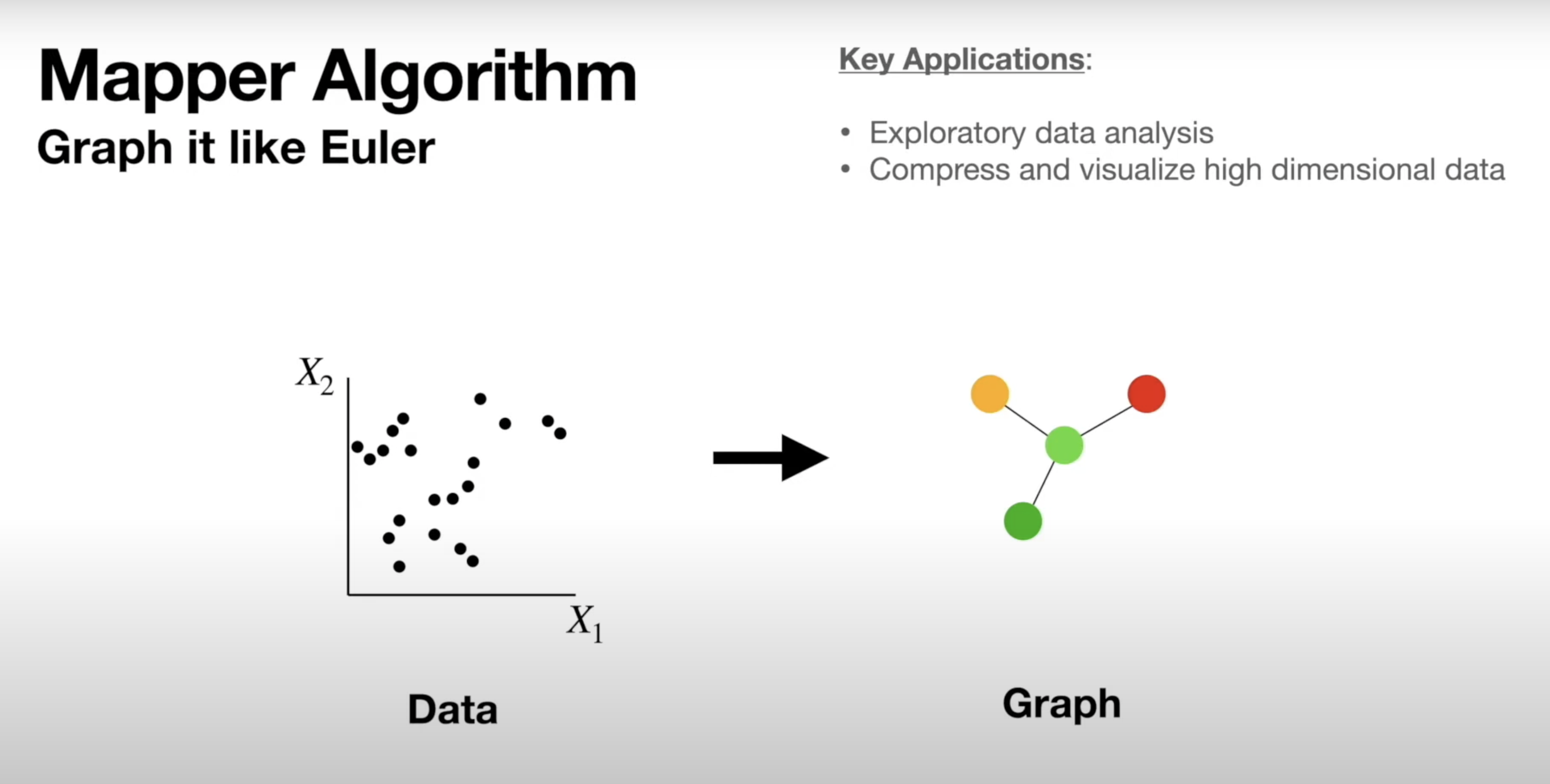
Mapper Algorithm

Mapper Algorithm

Mapper Algorithm
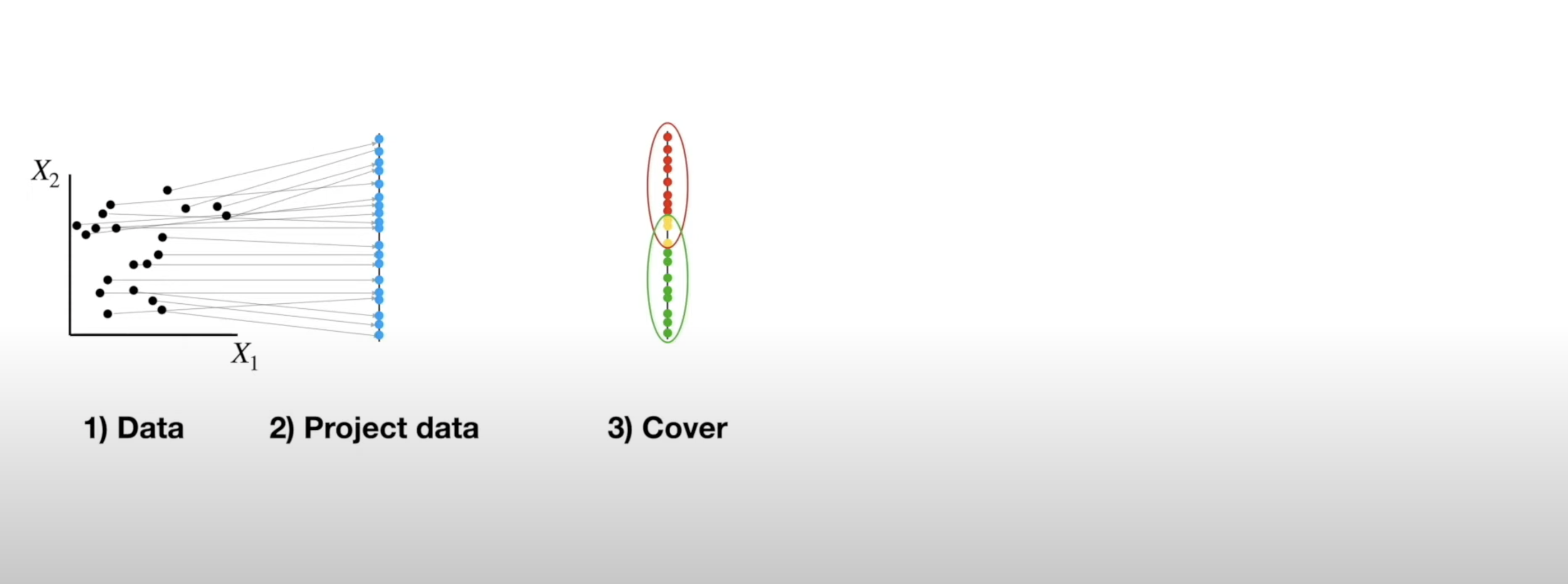
Mapper Algorithm
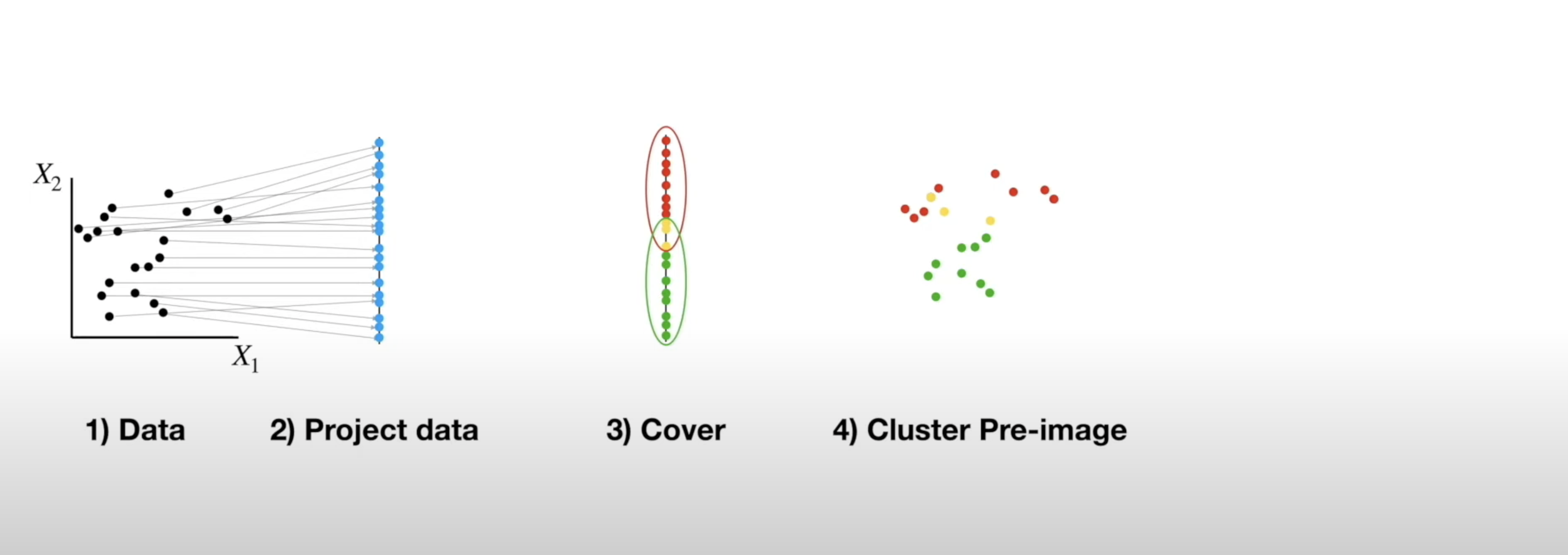
Mapper Algorithm
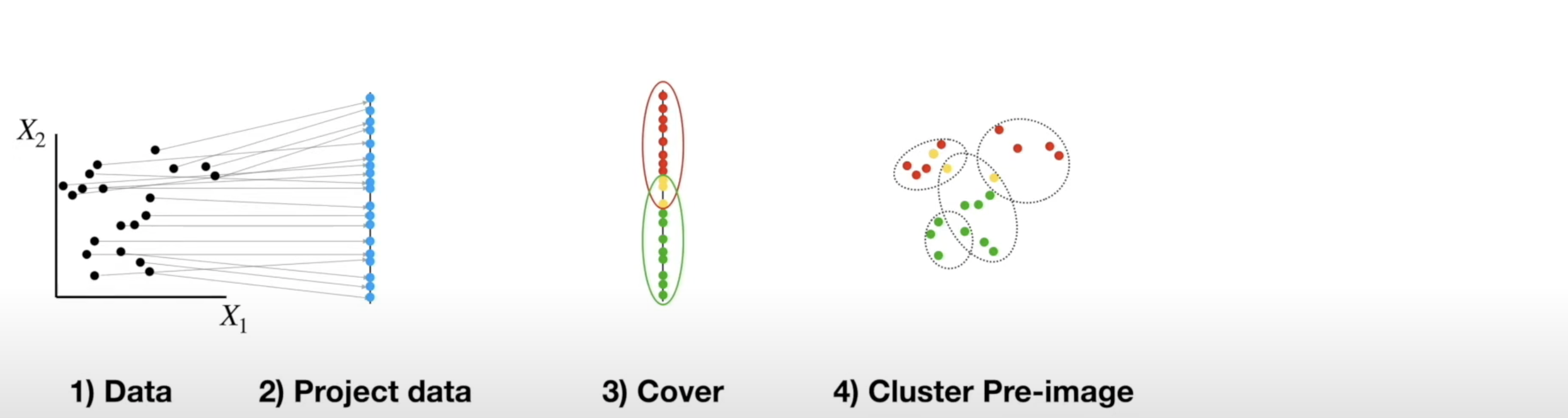
Mapper Algorithm
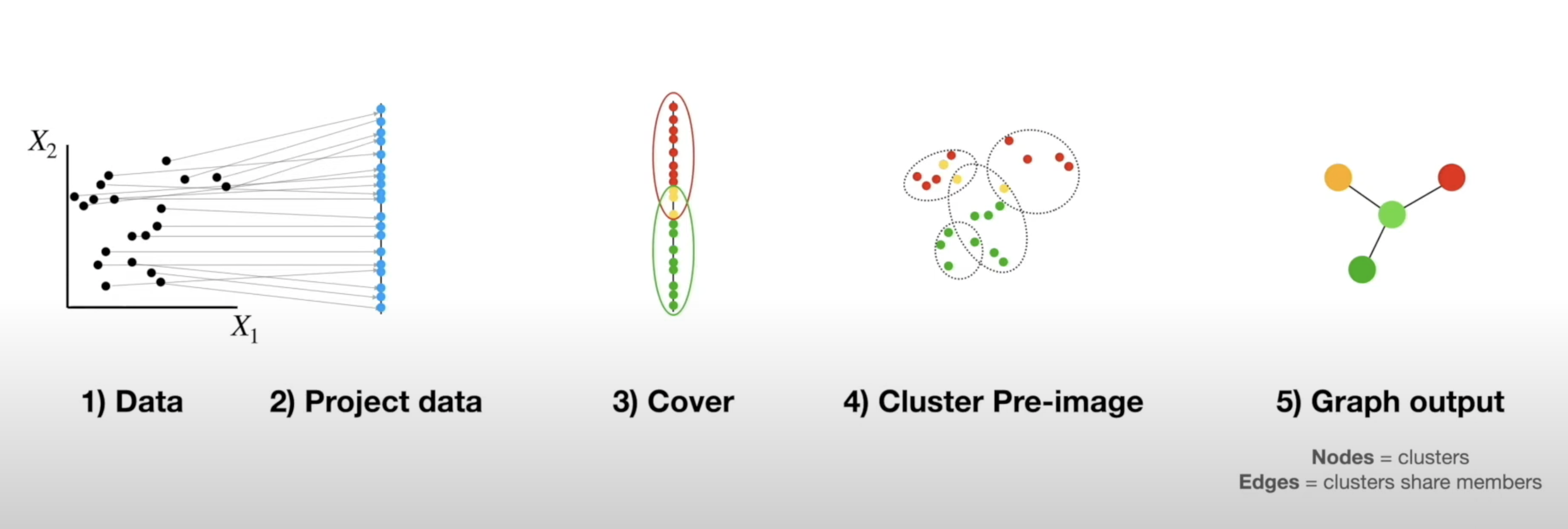
Example on Real Data in Python
Persistent Homology
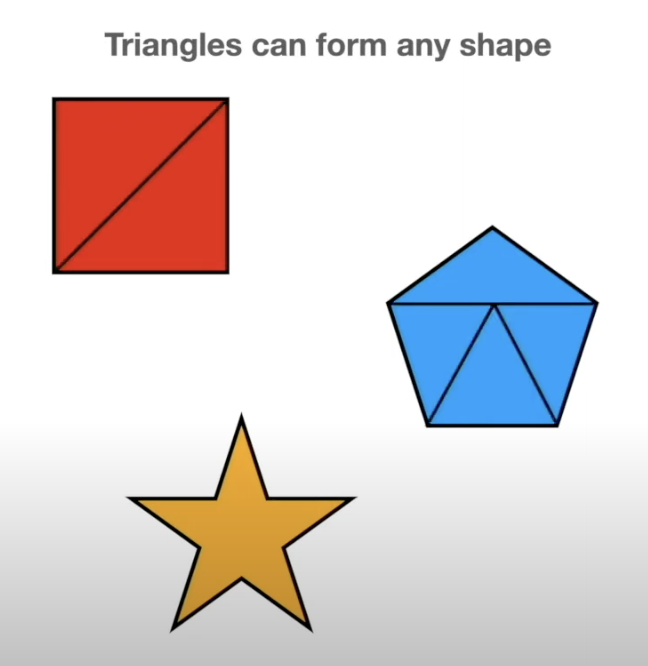
- TDA is about looking at the shape of data
- All polygons can be broken down into the simplest shape - a triangle
- If we want to analyze the shape of our data, we can break it down into triangles - this is the idea behind persistent homology
![]()
Persistent Homology
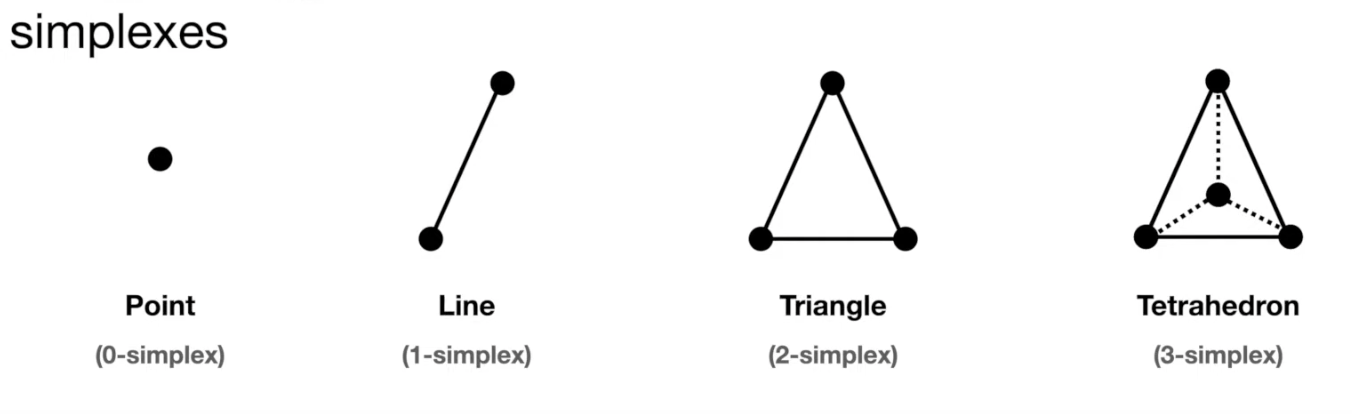
- But most datasets have more than two dimensions, so 2D triangles would not capture them
- Instead we use simplexes - triangles generalized to any number of dimensions
![]()
Persistent Homology
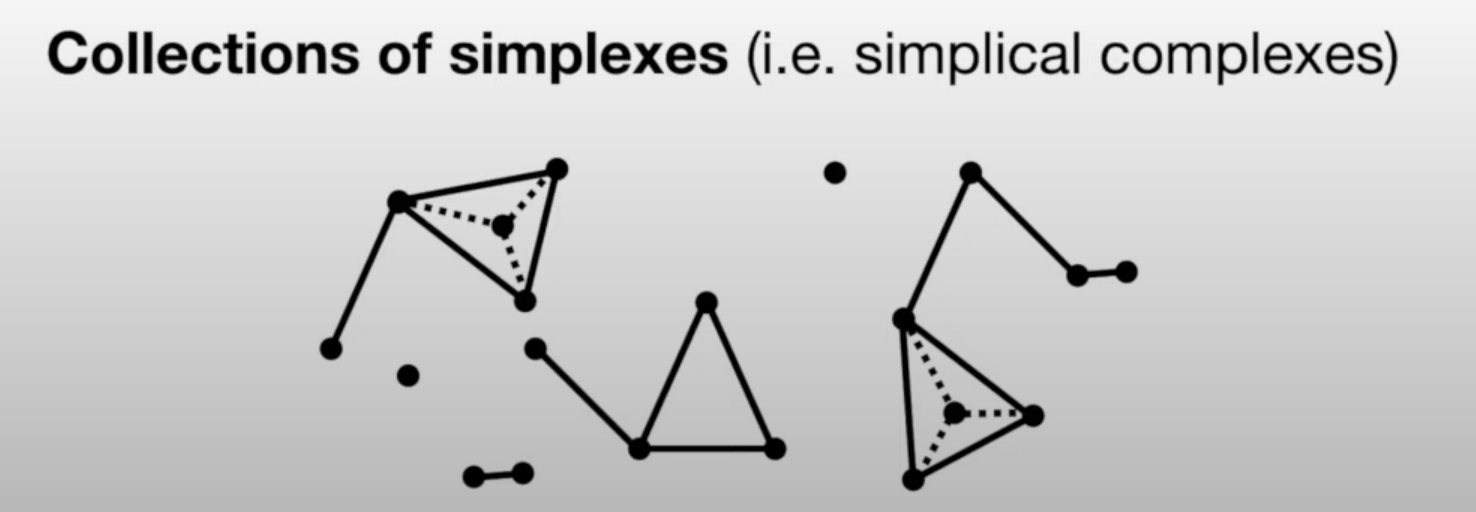
- We can use collections of simplexes (simplicial complexes) to describe our data
![]()
Persistent Homology
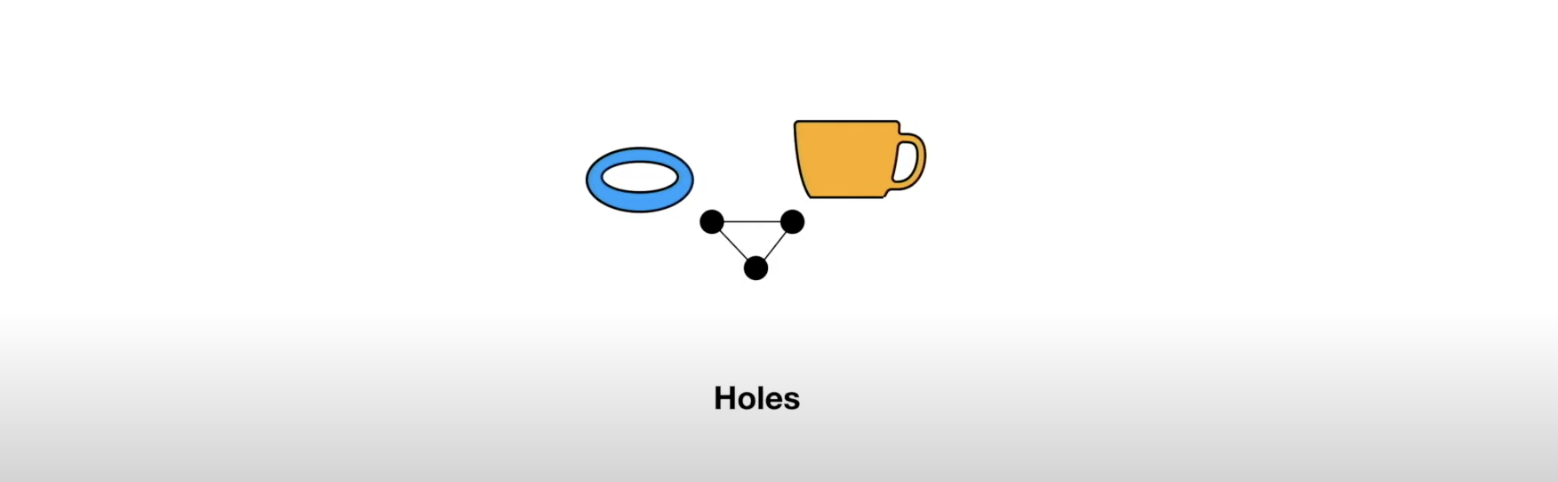
- How do we compare these complex shapes?
Persistent Homology
- How do we compare these complex shapes?
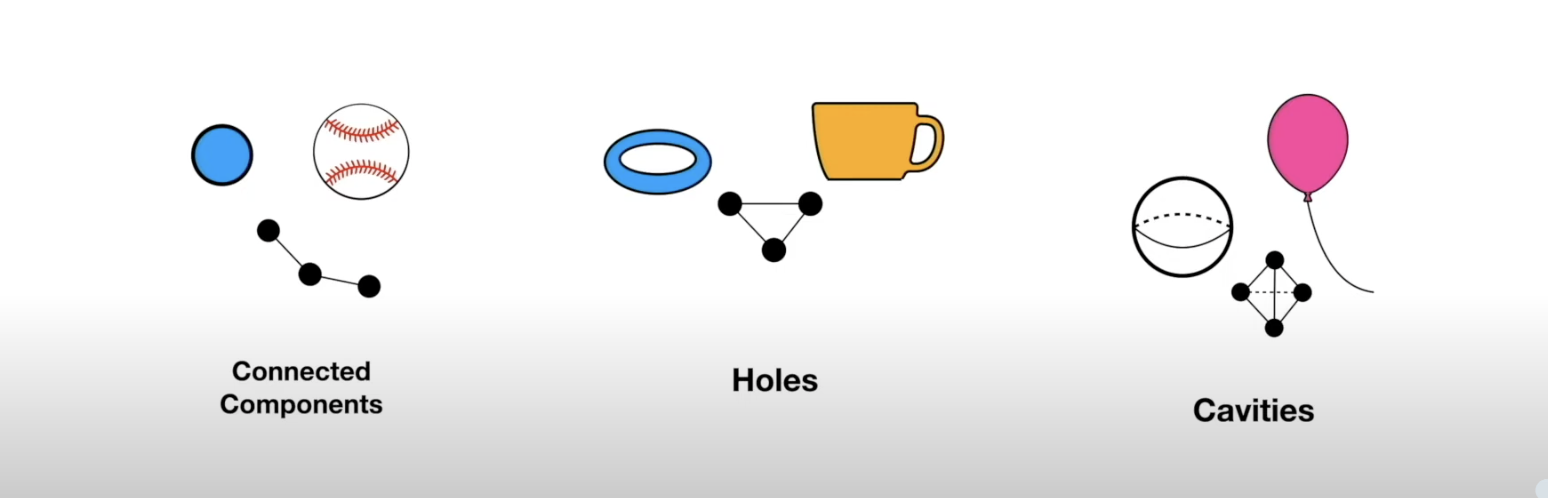
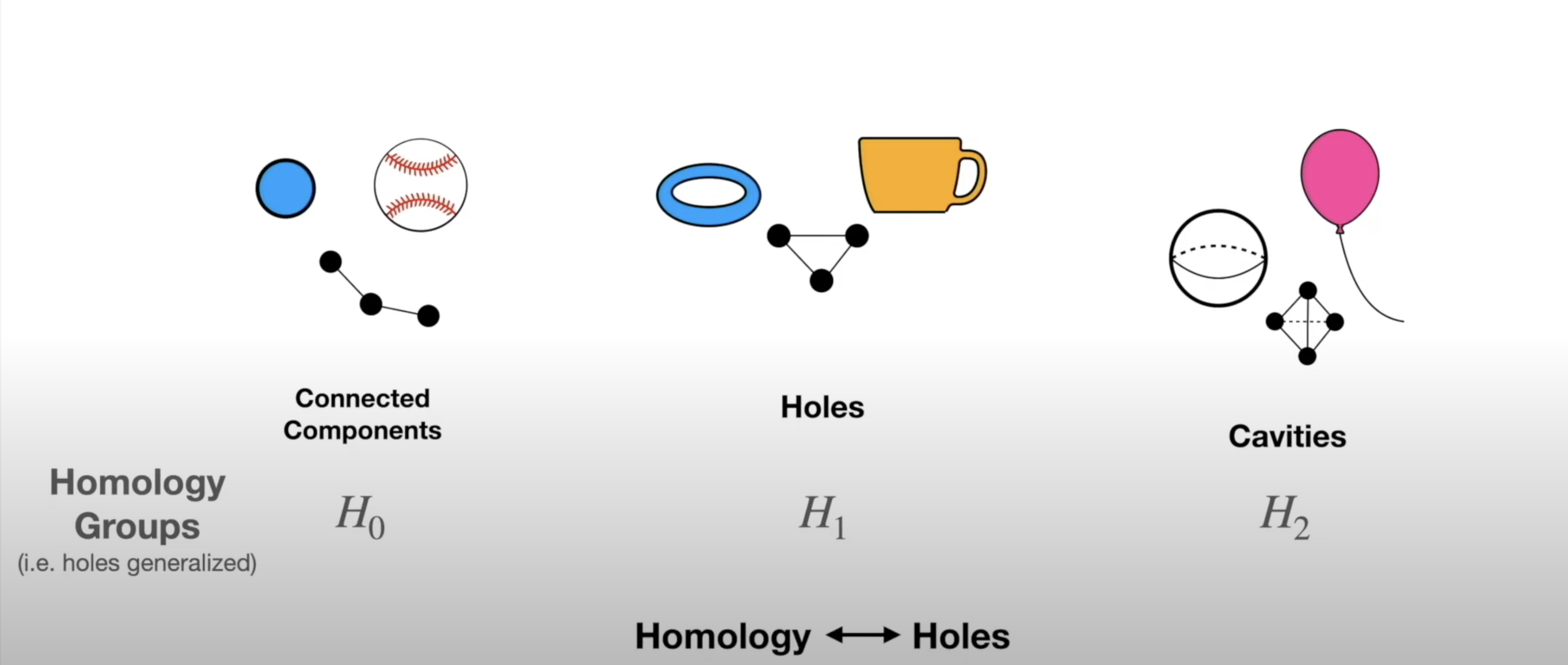
- These shapes can be characterized by their holes - we can compare them by counting their holes
![]()
Persistent Homology
- The concept of “hole” can also be generalized to any dimension:
![]()
Persistent Homology
- The concept of “hole” can also be generalized to any dimension (in 1 dimension we count connected components):
![]()
Persistent Homology
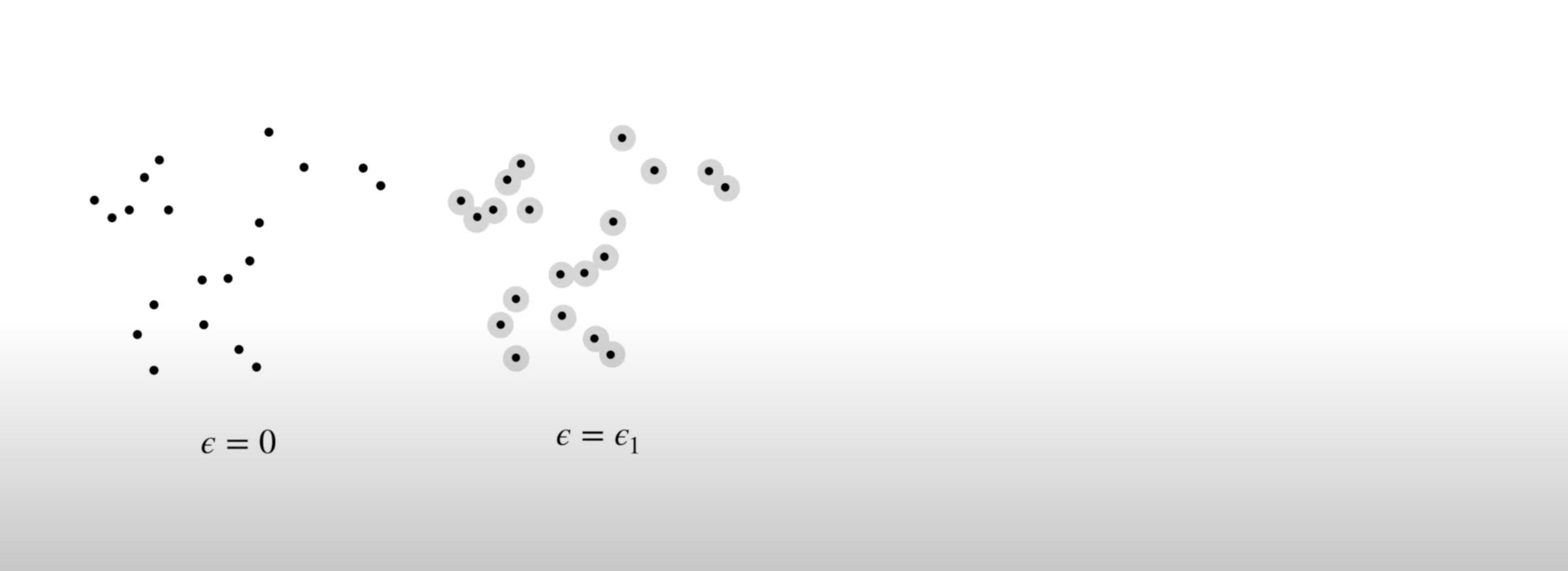
- To perform persistent homology, we first draw n-dimensional circles around each point:
![]()
Persistent Homology
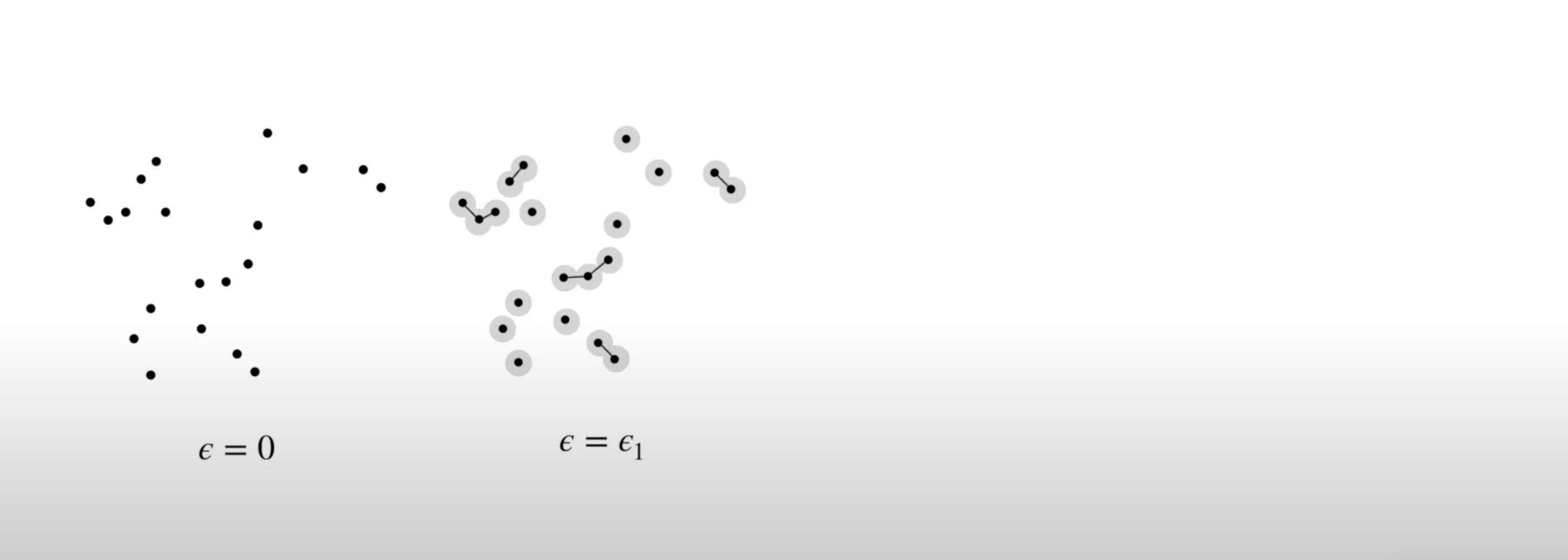
- We can then create 1-simplexes by connecting the data points whose circles overlap:
![]()
Persistent Homology
- Now we have two shapes: our initial 0-simplex (point cloud) and a shape made of 0- and 1-simplexes
![]()
Persistent Homology
- We can compare their homologies by counting the number of connected components:
![]()
Persistent Homology
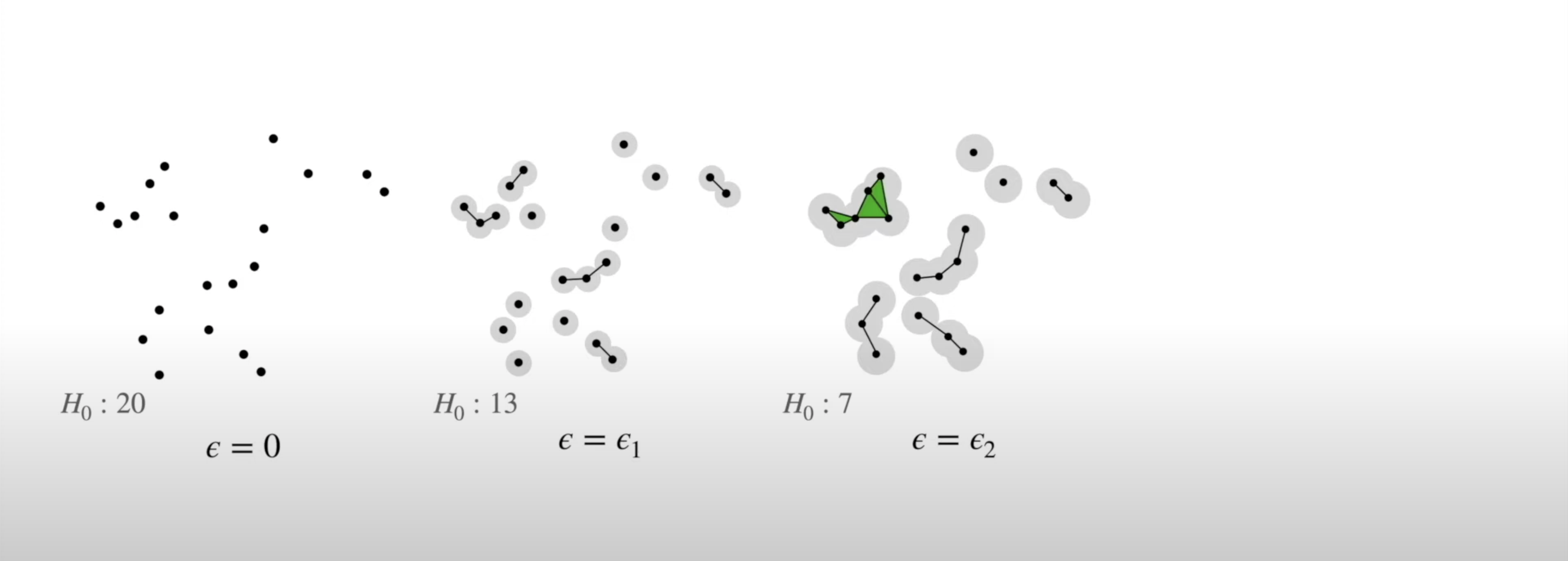
- We repeat this step, increasing the radius of the circles
- We see 2-simplexes start to appear and the number of connected components decreases:
![]()
Persistent Homology
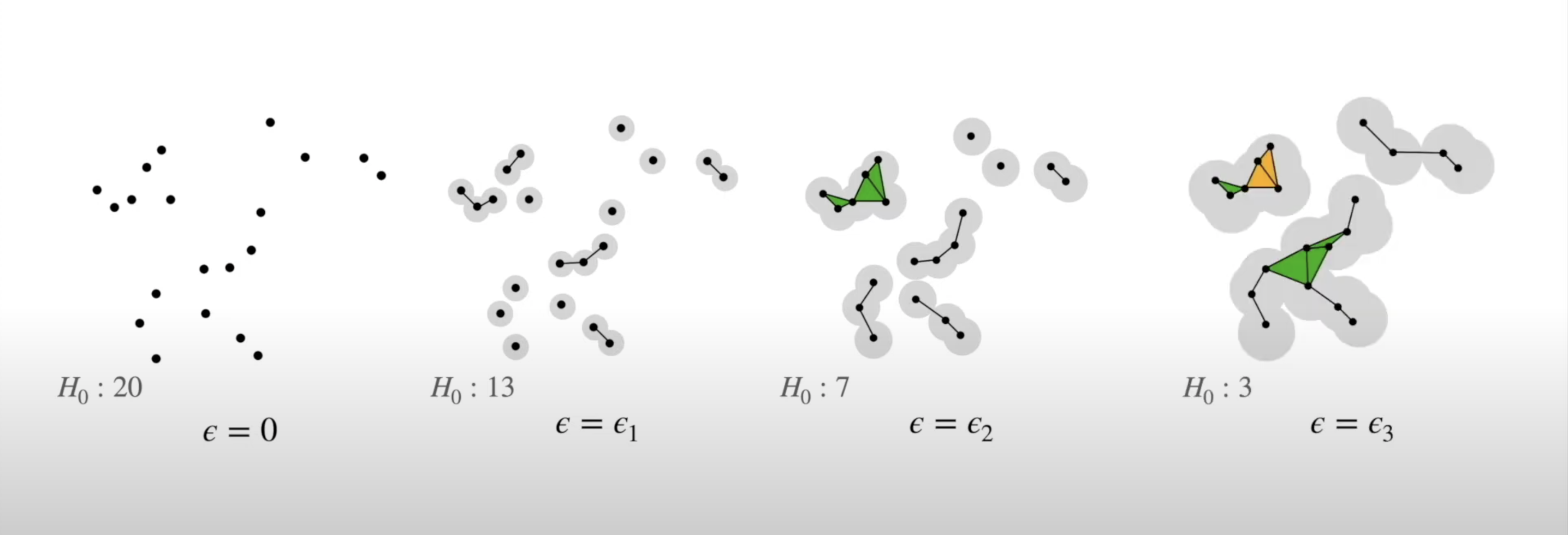
- We can do this for every choice of radius between 0 and the radius which yields only one connected component:
![]()
Persistent Homology
- This allows us to analyze which topological features of our data are significant based on how long they “persist” during the circle-growing process (longer persistence = more significant)
![]()
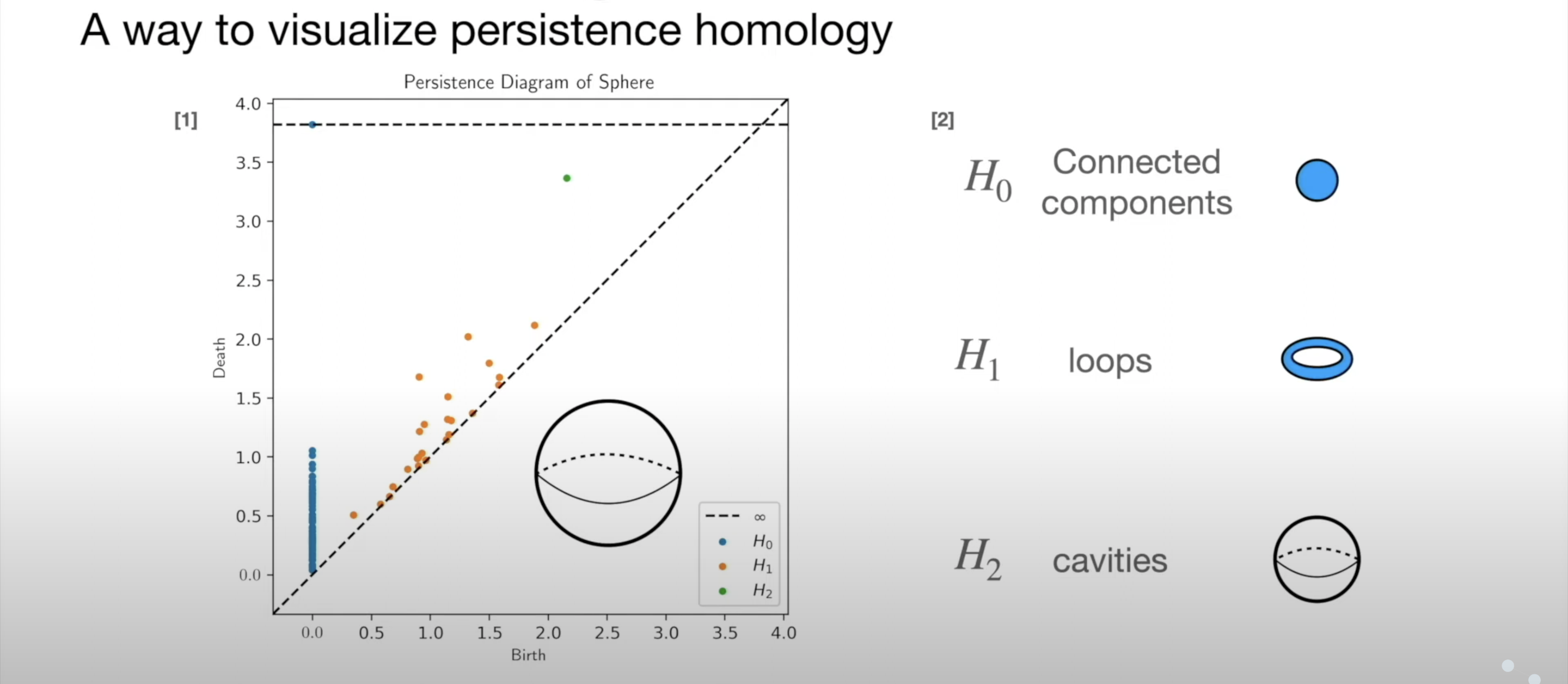
Persistence Diagram
- Points close to y=x are noise, points far from y=x are significant
![]()
Example on Real Data in Python
Further Reading
The original Mapper paper
Course notes for the 2021 EMAp summer course Topological Data Analysis with Persistent Homology
Rami Kraft’s Illustrations of Data Analysis Using the Mapper Algorithm and Persistent Homology
Shaw Talebi’s TDA video trilogy (this is a good starting point if you’re confused about anything)