Visualization for Machine Learning
## Agenda \ 1. Clustering 2. Dimensionality Reduction ## Clustering Etienne Bernard: "... the goal of clustering is to separate a set of examples into groups called clusters" 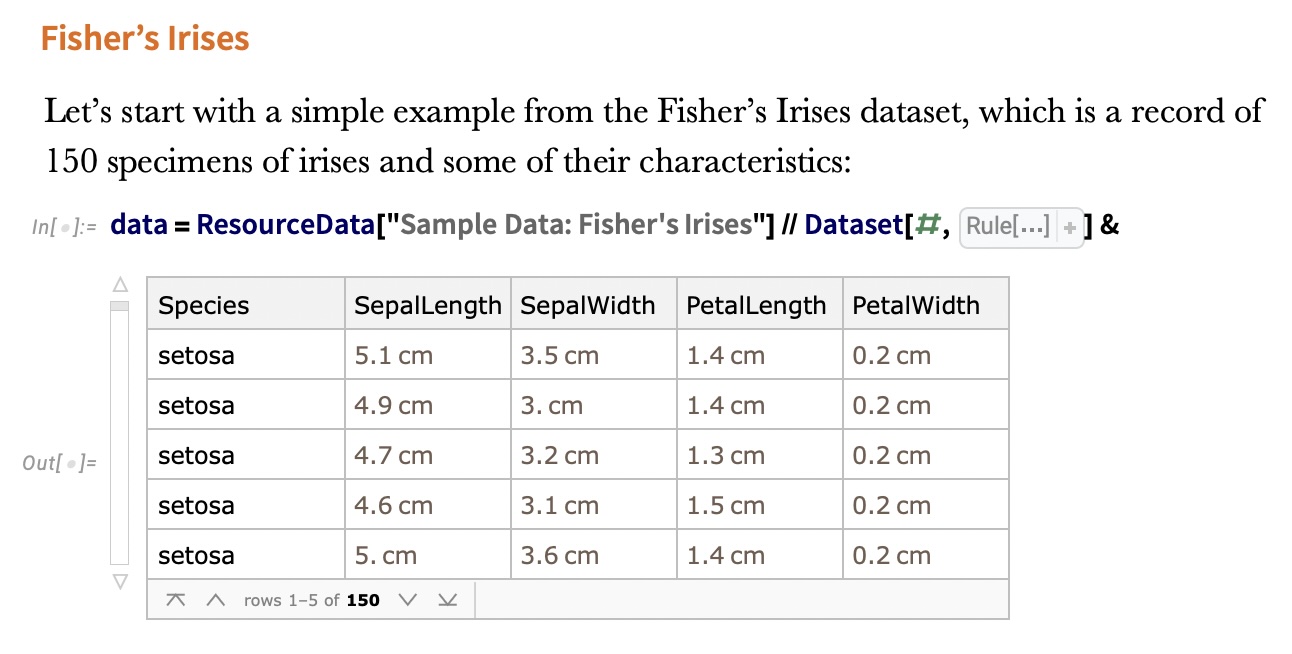 ## IRIS ``` python # Code source: Gaël Varoquaux # Modified for documentation by Jaques Grobler # License: BSD 3 clause # import matplotlib.pyplot as plt from sklearn import datasets iris = datasets.load_iris() _, ax = plt.subplots() scatter = ax.scatter(iris.data[:, 2], iris.data[:, 1]) ax.set(xlabel=iris.feature_names[2], ylabel=iris.feature_names[1]) _ = ax.legend( scatter.legend_elements()[0], iris.target_names, loc="lower right", title="Classes" ) ``` ## IRIS ```{python} import matplotlib.pyplot as plt from sklearn import datasets iris = datasets.load_iris() _, ax = plt.subplots() scatter = ax.scatter(iris.data[:, 2], iris.data[:, 1]) ax.set(xlabel=iris.feature_names[2], ylabel=iris.feature_names[1]) _ = ax.legend( scatter.legend_elements()[0], iris.target_names, loc="lower right", title="Classes" ) ``` ## IRIS -- another look (Bernard) 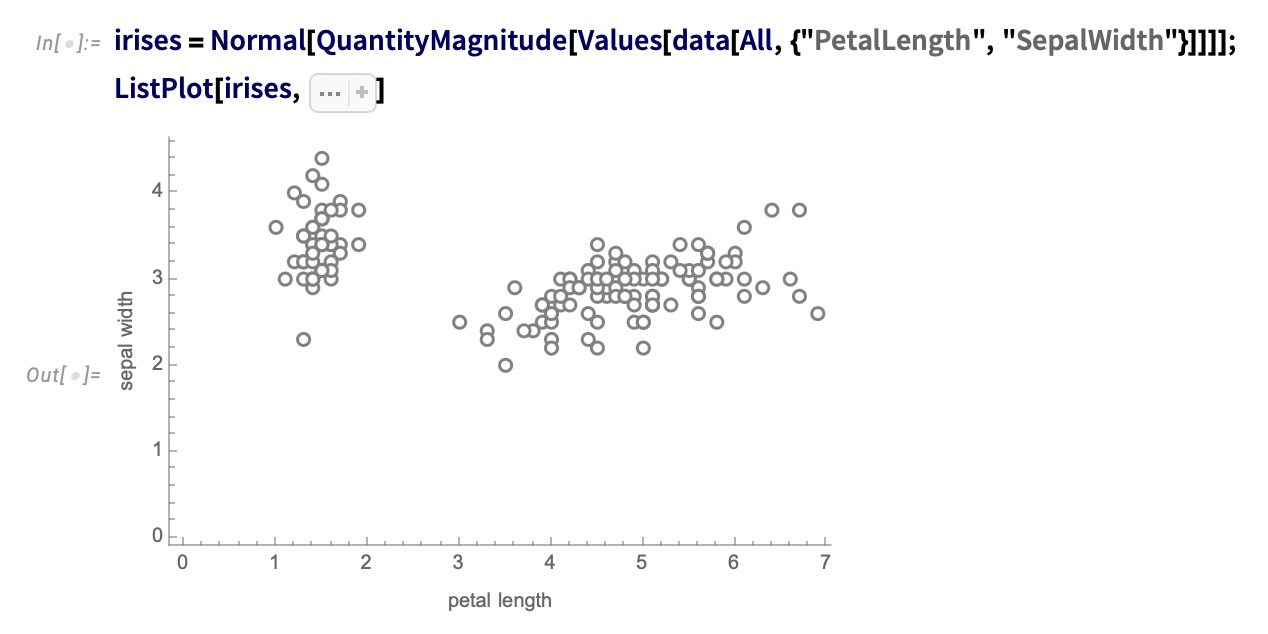 ## IRIS -- clustering 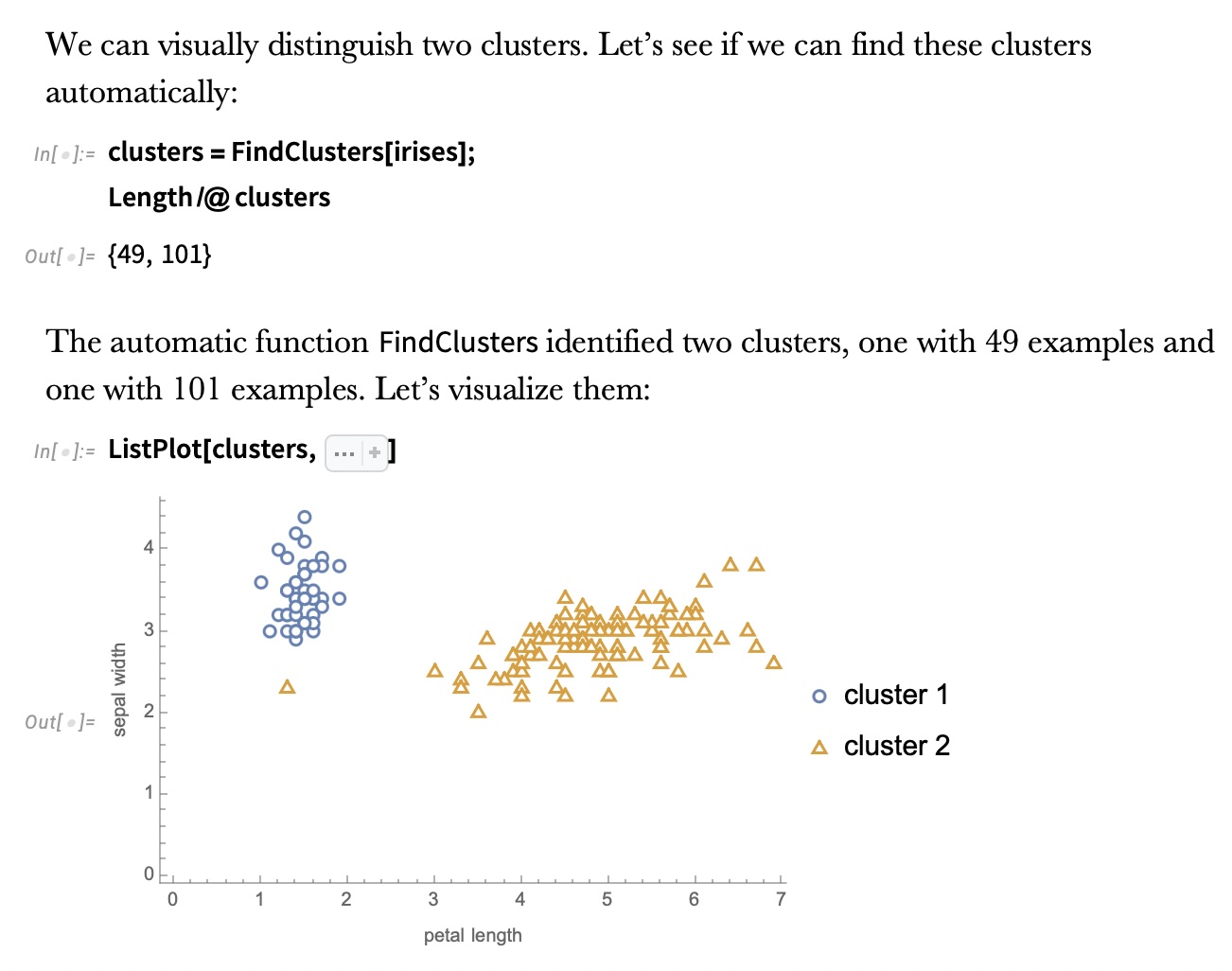 ## IRIS -- k-means 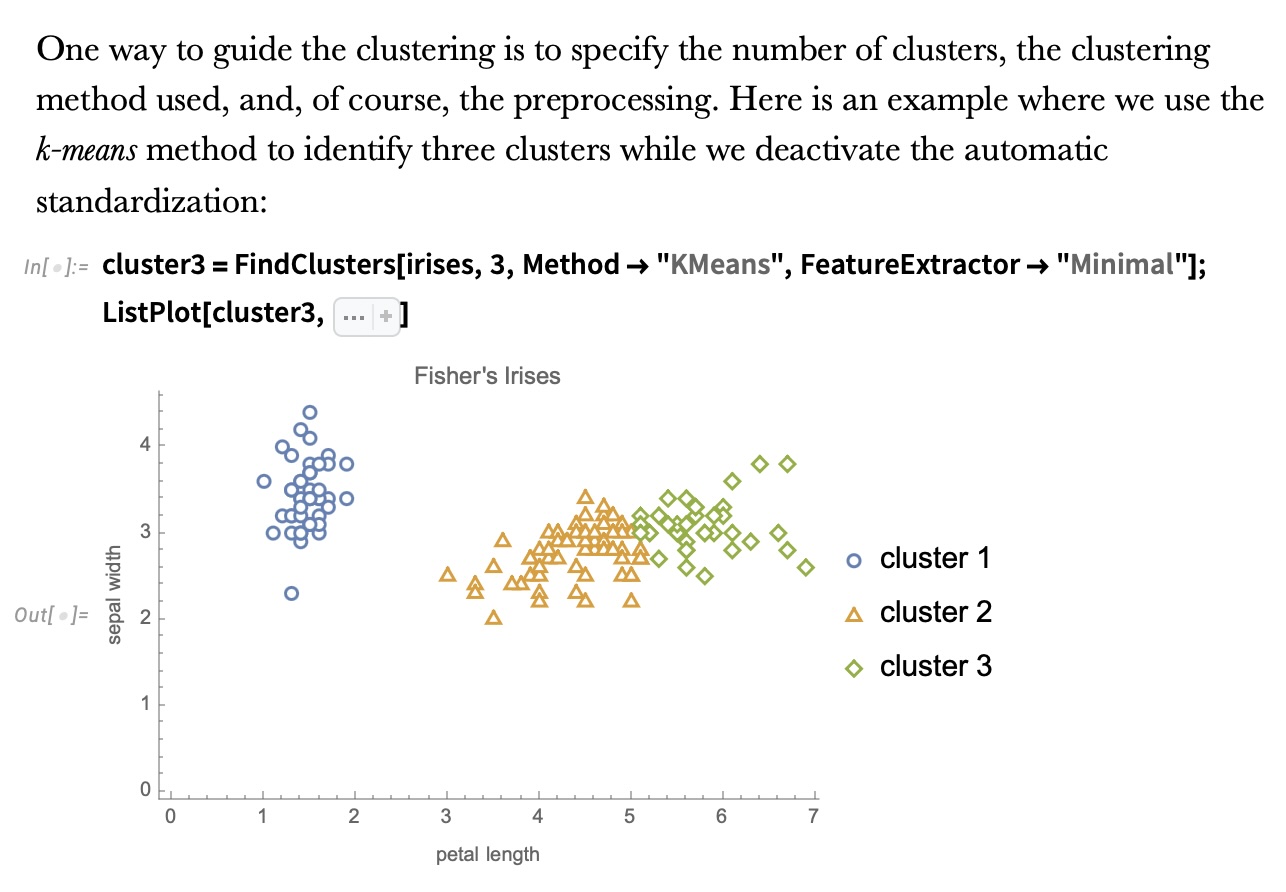 ## Wolfram Mathematica FindClusters 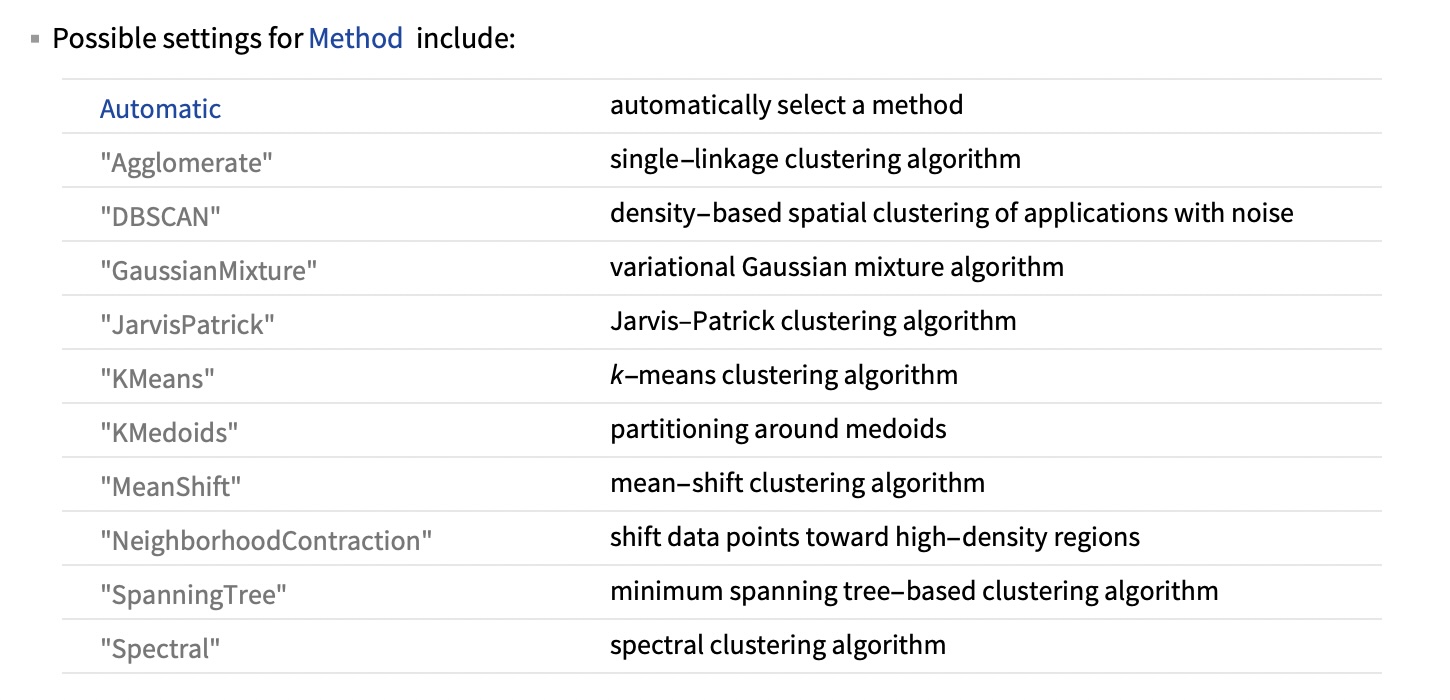 ## Wolfram Mathematica FindClusters 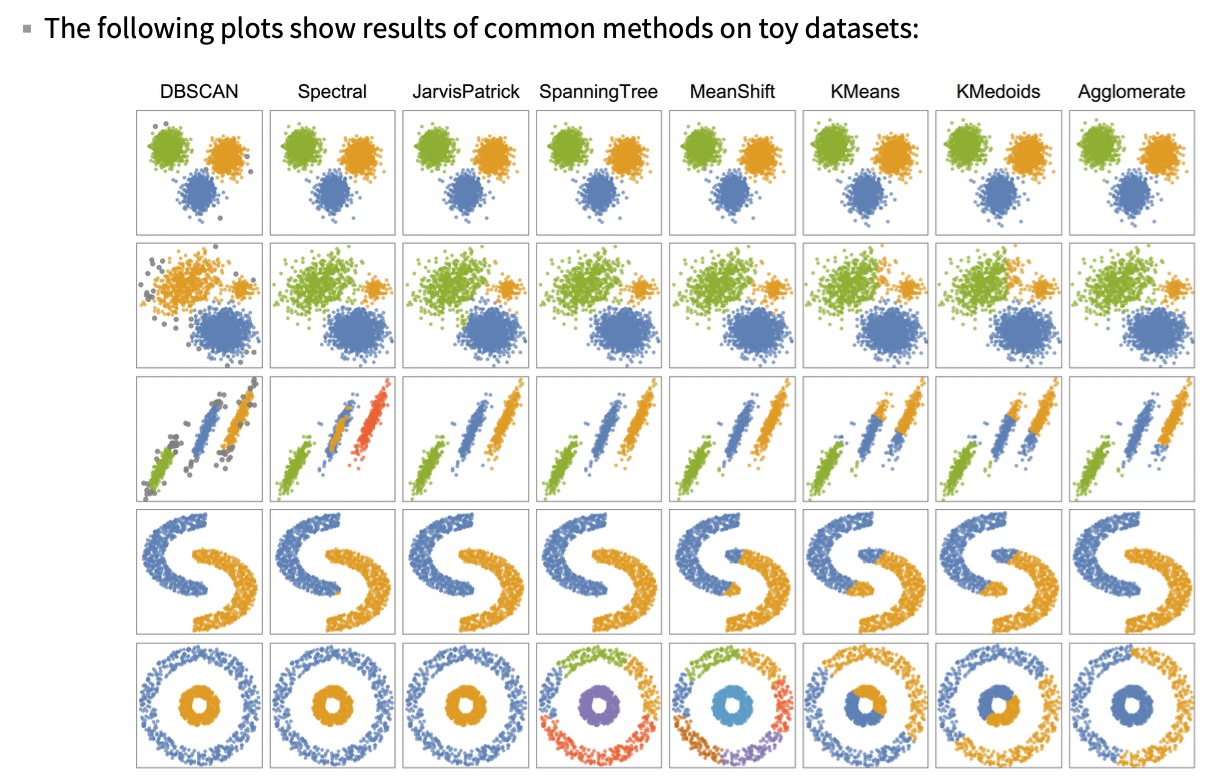 ## IRIS - classes :::: {.columns} ::: {.column width="50%"} ```{python} import matplotlib.pyplot as plt from sklearn import datasets iris = datasets.load_iris() _, ax = plt.subplots() scatter = ax.scatter(iris.data[:, 2], iris.data[:, 1], c=iris.target) ax.set(xlabel=iris.feature_names[2], ylabel=iris.feature_names[1]) _ = ax.legend( scatter.legend_elements()[0], iris.target_names, loc="lower right", title="Classes" ) ``` ::: ::: {.column width="50%"} 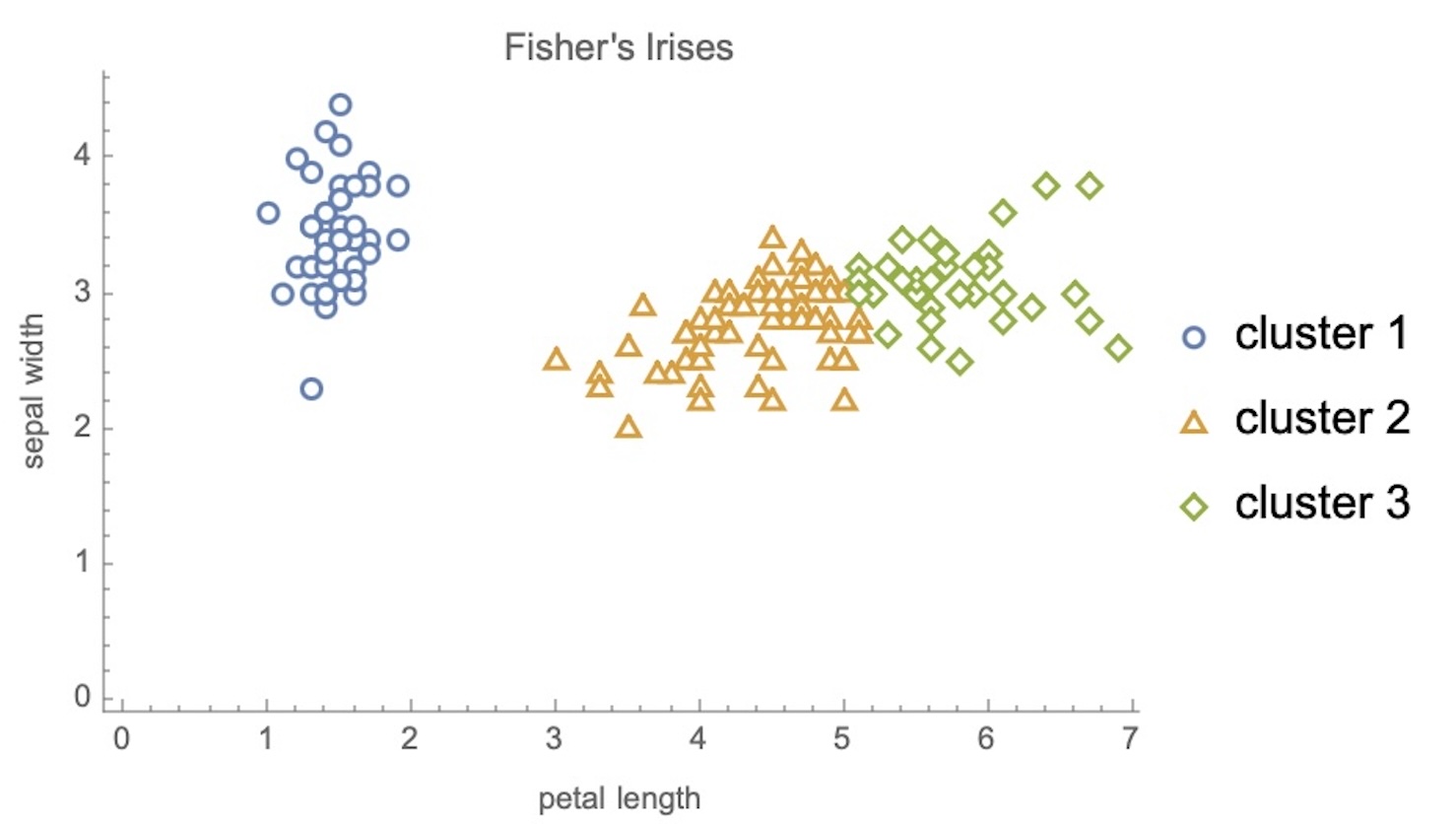 ::: :::: ## Recommended reading * **Required** https://www.wolfram.com/language/introduction-machine-learning/clustering/ [link](https://www.wolfram.com/language/introduction-machine-learning/clustering/) * https://en.wikipedia.org/wiki/Cluster_analysis * https://en.wikipedia.org/wiki/K-means_clustering * https://en.wikipedia.org/wiki/DBSCAN ## Dimensionality Reduction * Input data may have thousands or millions of dimensions! * **Dimensionality Reduction** represents data with fewer dimensions - easier learning -- fewer parameters - visualization -- show high-dimensional data in 2D or 3D - discover "intrinsic dimensionality" of the data ## Dimensionality Reduction (Yi Zhang) * Assumption: data lies on a lower dimensional space 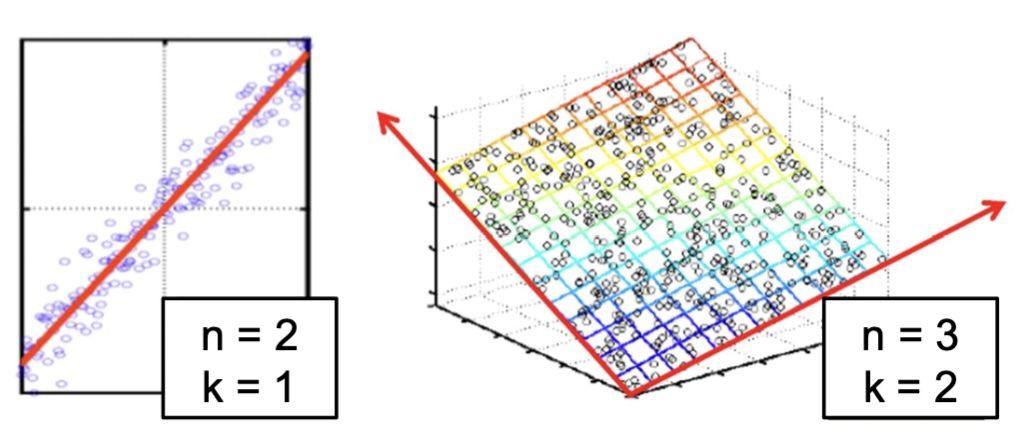 ## Dimensionality Reduction (Bishop) * Supposed a dataset of "3s" perturbed in various ways  * What operations did we perform? What's the intrinsic dimensionality? * Here the underlying **manifold** is **non-linear** ## Digits ``` python from sklearn.datasets import load_digits digits = load_digits(n_class=6) X, y = digits.data, digits.target ``` ## Digits - 0 ```{python} from sklearn.datasets import load_digits digits = load_digits(n_class=6) digits.images[0] ``` ## Digits - 1 ```{python} from sklearn.datasets import load_digits digits = load_digits(n_class=6) digits.images[1] ``` ## Digits ```{python} from sklearn.datasets import load_digits digits = load_digits(n_class=6) X, y = digits.data, digits.target n_samples, n_features = X.shape n_neighbors = 30 import matplotlib.pyplot as plt fig, axs = plt.subplots(nrows=10, ncols=10, figsize=(6, 6)) for idx, ax in enumerate(axs.ravel()): ax.imshow(X[idx].reshape((8, 8)), cmap=plt.cm.binary) ax.axis("off") _ = fig.suptitle("A selection from the 64-dimensional digits dataset", fontsize=16) ``` ## Digits ```{python} import numpy as np from matplotlib import offsetbox from sklearn.preprocessing import MinMaxScaler def plot_embedding(X, title): _, ax = plt.subplots() X = MinMaxScaler().fit_transform(X) for digit in digits.target_names: ax.scatter( *X[y == digit].T, marker=f"${digit}$", s=60, color=plt.cm.Dark2(digit), alpha=0.425, zorder=2, ) shown_images = np.array([[1.0, 1.0]]) # just something big for i in range(X.shape[0]): # plot every digit on the embedding # show an annotation box for a group of digits dist = np.sum((X[i] - shown_images) ** 2, 1) if np.min(dist) < 4e-3: # don't show points that are too close continue shown_images = np.concatenate([shown_images, [X[i]]], axis=0) imagebox = offsetbox.AnnotationBbox( offsetbox.OffsetImage(digits.images[i], cmap=plt.cm.gray_r), X[i] ) imagebox.set(zorder=1) ax.add_artist(imagebox) ax.set_title(title) ax.axis("off") from sklearn.decomposition import TruncatedSVD from sklearn.discriminant_analysis import LinearDiscriminantAnalysis from sklearn.ensemble import RandomTreesEmbedding from sklearn.manifold import ( MDS, TSNE, Isomap, LocallyLinearEmbedding, SpectralEmbedding, ) from sklearn.neighbors import NeighborhoodComponentsAnalysis from sklearn.pipeline import make_pipeline from sklearn.random_projection import SparseRandomProjection embeddings = { "Random projection embedding": SparseRandomProjection( n_components=2, random_state=42 ), "Truncated SVD embedding": TruncatedSVD(n_components=2), "Linear Discriminant Analysis embedding": LinearDiscriminantAnalysis( n_components=2 ), "Isomap embedding": Isomap(n_neighbors=n_neighbors, n_components=2), "Standard LLE embedding": LocallyLinearEmbedding( n_neighbors=n_neighbors, n_components=2, method="standard" ), "Modified LLE embedding": LocallyLinearEmbedding( n_neighbors=n_neighbors, n_components=2, method="modified" ), "Hessian LLE embedding": LocallyLinearEmbedding( n_neighbors=n_neighbors, n_components=2, method="hessian" ), "LTSA LLE embedding": LocallyLinearEmbedding( n_neighbors=n_neighbors, n_components=2, method="ltsa" ), "MDS embedding": MDS(n_components=2, n_init=1, max_iter=120, n_jobs=2), "Random Trees embedding": make_pipeline( RandomTreesEmbedding(n_estimators=200, max_depth=5, random_state=0), TruncatedSVD(n_components=2), ), "Spectral embedding": SpectralEmbedding( n_components=2, random_state=0, eigen_solver="arpack" ), "t-SNE embedding": TSNE( n_components=2, n_iter=500, n_iter_without_progress=150, n_jobs=2, random_state=0, ), "NCA embedding": NeighborhoodComponentsAnalysis( n_components=2, init="pca", random_state=0 ), } from time import time projections, timing = {}, {} for name, transformer in embeddings.items(): if name.startswith("Linear Discriminant Analysis"): data = X.copy() data.flat[:: X.shape[1] + 1] += 0.01 # Make X invertible else: data = X print(f"Computing {name}...") start_time = time() projections[name] = transformer.fit_transform(data, y) timing[name] = time() - start_time for name in timing: if name=="t-SNE embedding": title = f"{name} (time {timing[name]:.3f}s)" plot_embedding(projections[name], title) plt.show() ``` ## Principal Component Analysis (Luis Gustavo Nonato) ::: incremental - PCA is directly related to the eigenvectors and eigenvalues of covariance matrices. - Lets so make a quick review of eigenvectors, eigenvalues, and covariance matrices. ::: ## Eigenvectors and Eigenvalues Given a $d \times d$ matrix $A$, a pair $(\lambda, u)$ that satisfies $A u = \lambda u$ is called eigenvalue $\lambda$ and corresponding eigenvector $u$ of $A$. ## Symmetric Matrices - $\lambda \in \mathbb{R}$ and $u \in \mathbb{R}^d$ (no complex numbers involved) - The eigenvectors are orthogonal 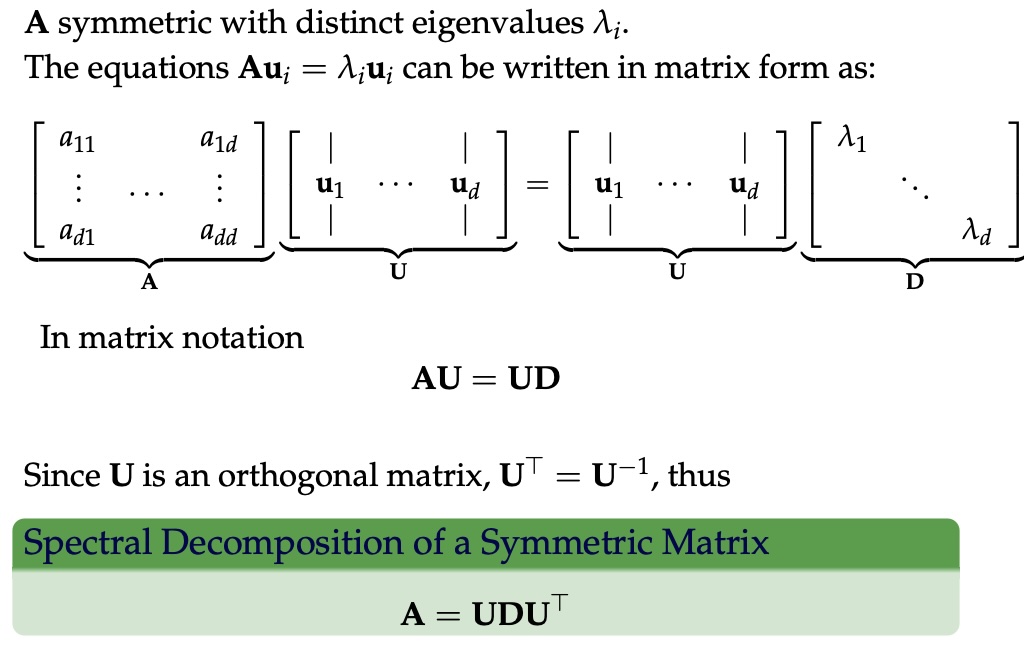 ## Covariance Matrix  ## Covariance Matrix :::: {.columns} ::: {.column width="50%"} 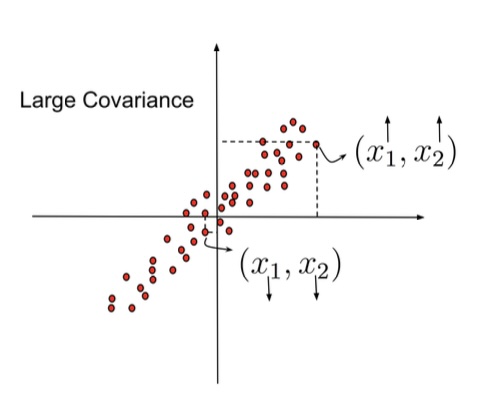 ::: ::: {.column width="50%"} 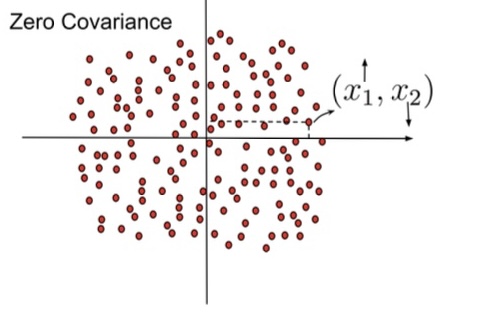 ::: :::: ## Covariance Matrix  ## Principal Component Analysis: intuition 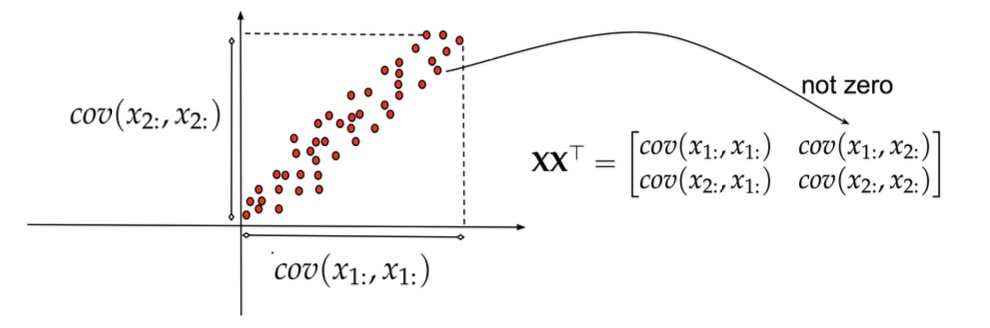 ## Principal Component Analysis: intuition 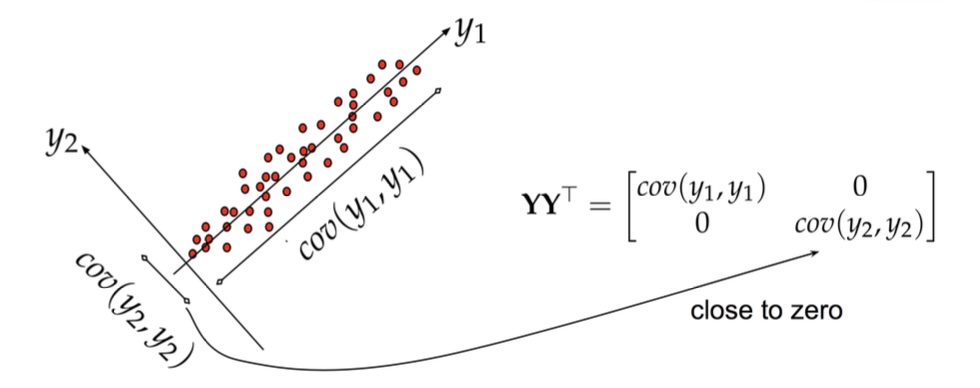 ## Principal Component Analysis  ## Principal Component Analysis 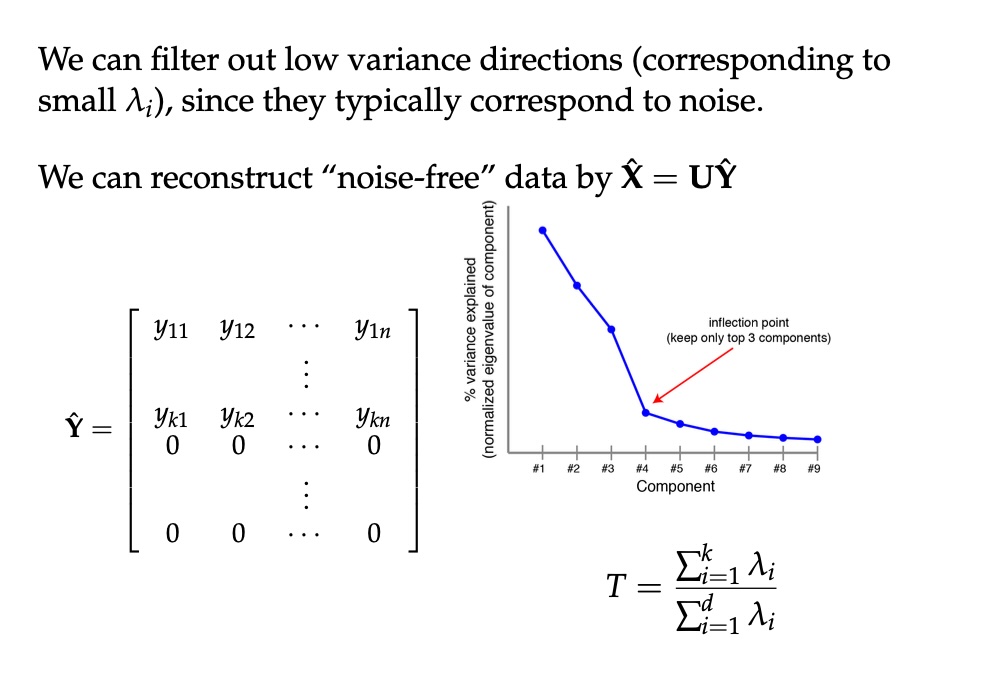 ## PCA of digits ```{python} from sklearn.decomposition import PCA pca = PCA(n_components=2) data, labels = load_digits(return_X_y=True) reduced_data=pca.fit_transform(data) plt.scatter(reduced_data[:, 0], reduced_data[:, 1]) plt.show() ``` ## PCA of digits ```{python} from sklearn.decomposition import PCA pca = PCA(n_components=2) data, labels = load_digits(return_X_y=True) reduced_data=pca.fit_transform(data) plt.scatter(reduced_data[:, 0], reduced_data[:, 1], c=labels) plt.show() ``` ## Scaling Up * Covariance matrix can be really big! - $\Sigma$ is $n$ by $n$ - 10000 features are not uncommon - computing eigenvectors is slow... * Solution: Singular Value Decomposition (SVD) - Finds the $k$ largest eigenvectors - Widely implemented robustly in major packages ## Singular Value Decomposition (SVD) * https://en.wikipedia.org/wiki/Singular_value_decomposition 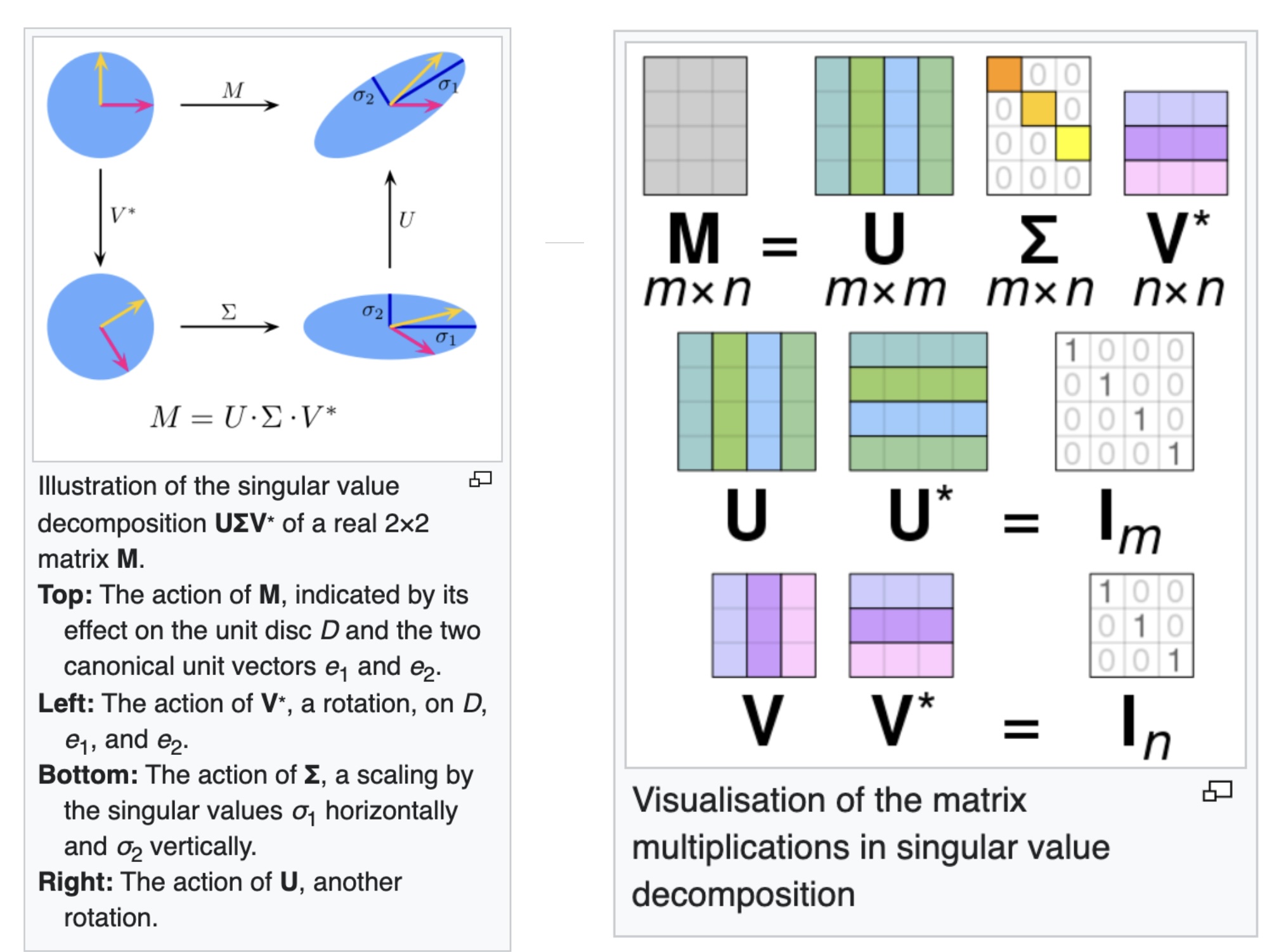 ## Dimensionality Reduction Techniques * https://en.wikipedia.org/wiki/Dimensionality_reduction - Principal component analysis (PCA) - Non-negative matrix factorization (NMF) - Linear discriminant analysis (LDA) - t-SNE - UMAP - **many others** ## Local Linear Embedding 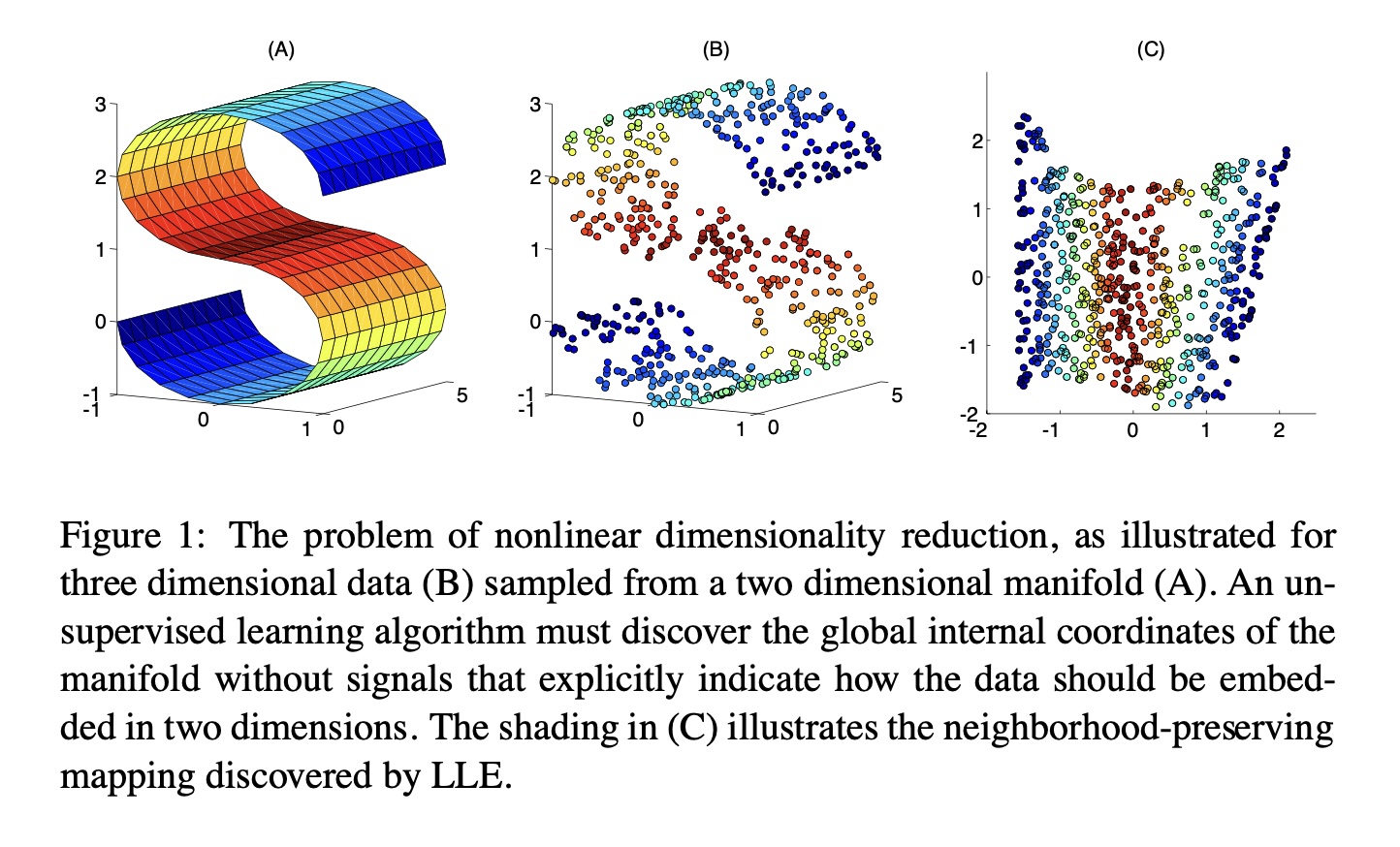 ## Preserving Local Manifold Neighborhoods 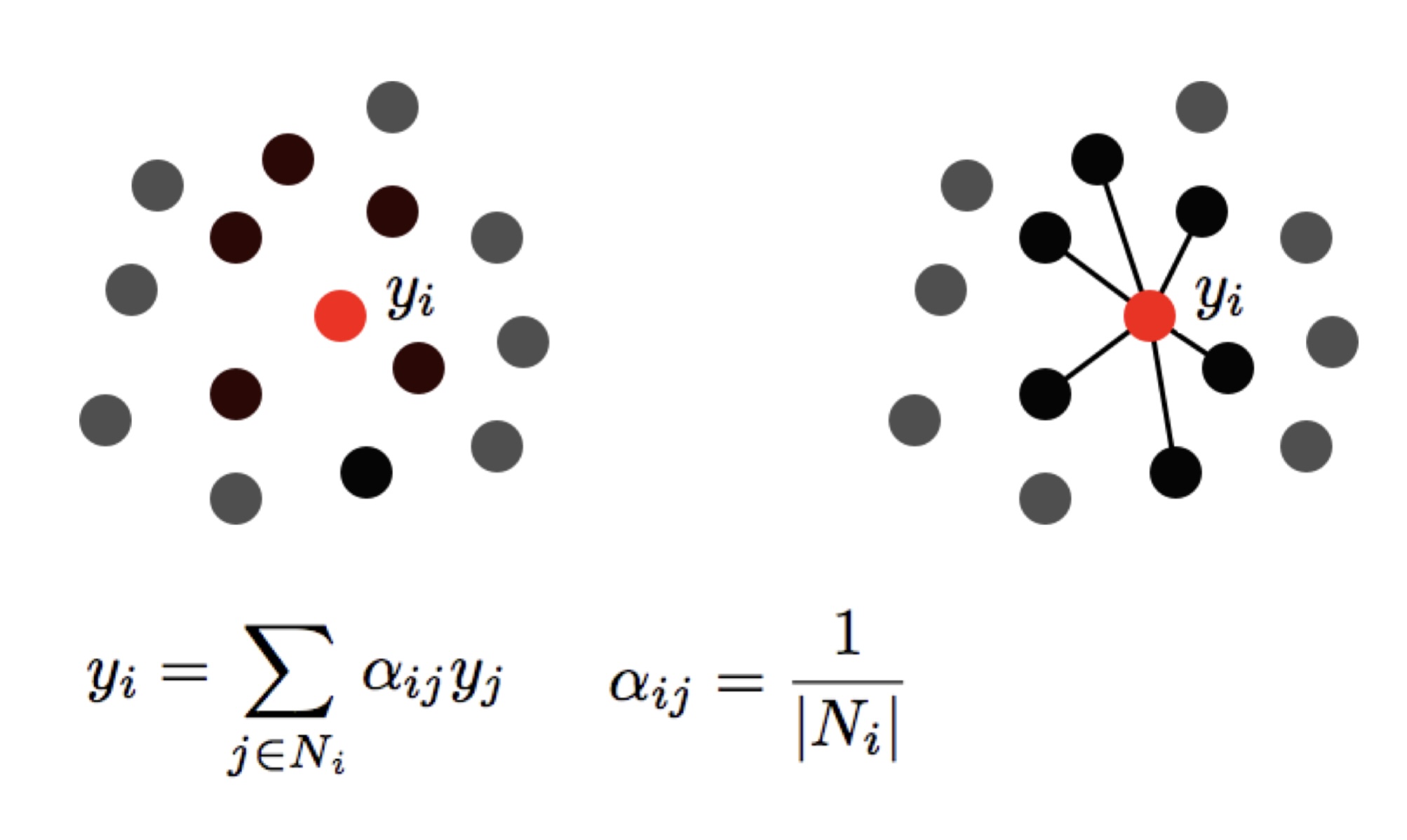 ## LLE  https://www.science.org/doi/10.1126/science.290.5500.2323 ## PCA vs LLE 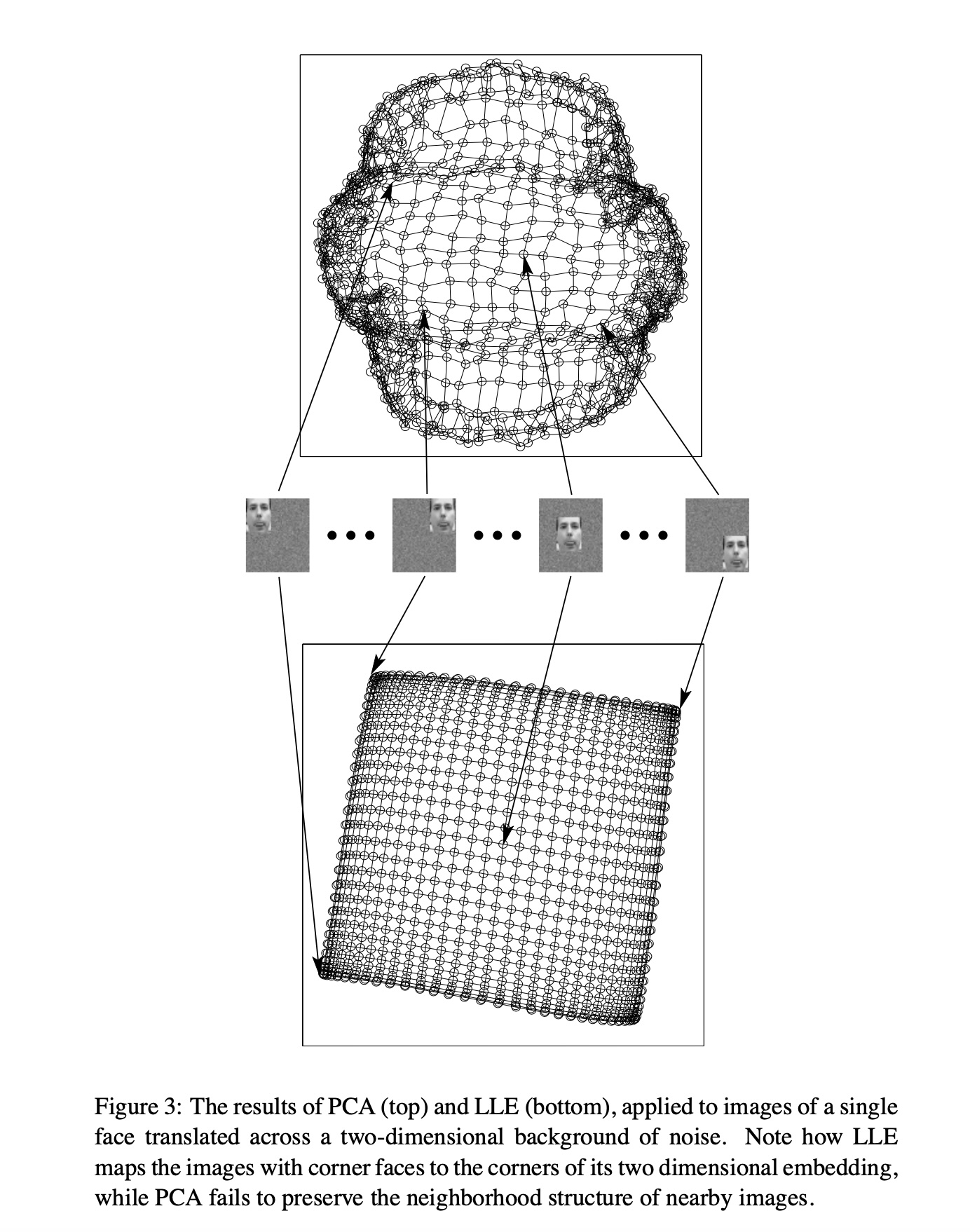{height="600"} ## Graph Layout using force based approach [video link](https://www.youtube.com/watch?v=_Oidv5M-fuw) ## SNE and t-SNE :::: {.columns} ::: {.column width="50%"}  ::: ::: {.column width="40%"}  ::: :::: HERE is an excellent talk by t-SNE creator: [video link](https://www.youtube.com/watch?v=RJVL80Gg3lA&list=UUtXKDgv1AVoG88PLl8nGXmw) ## 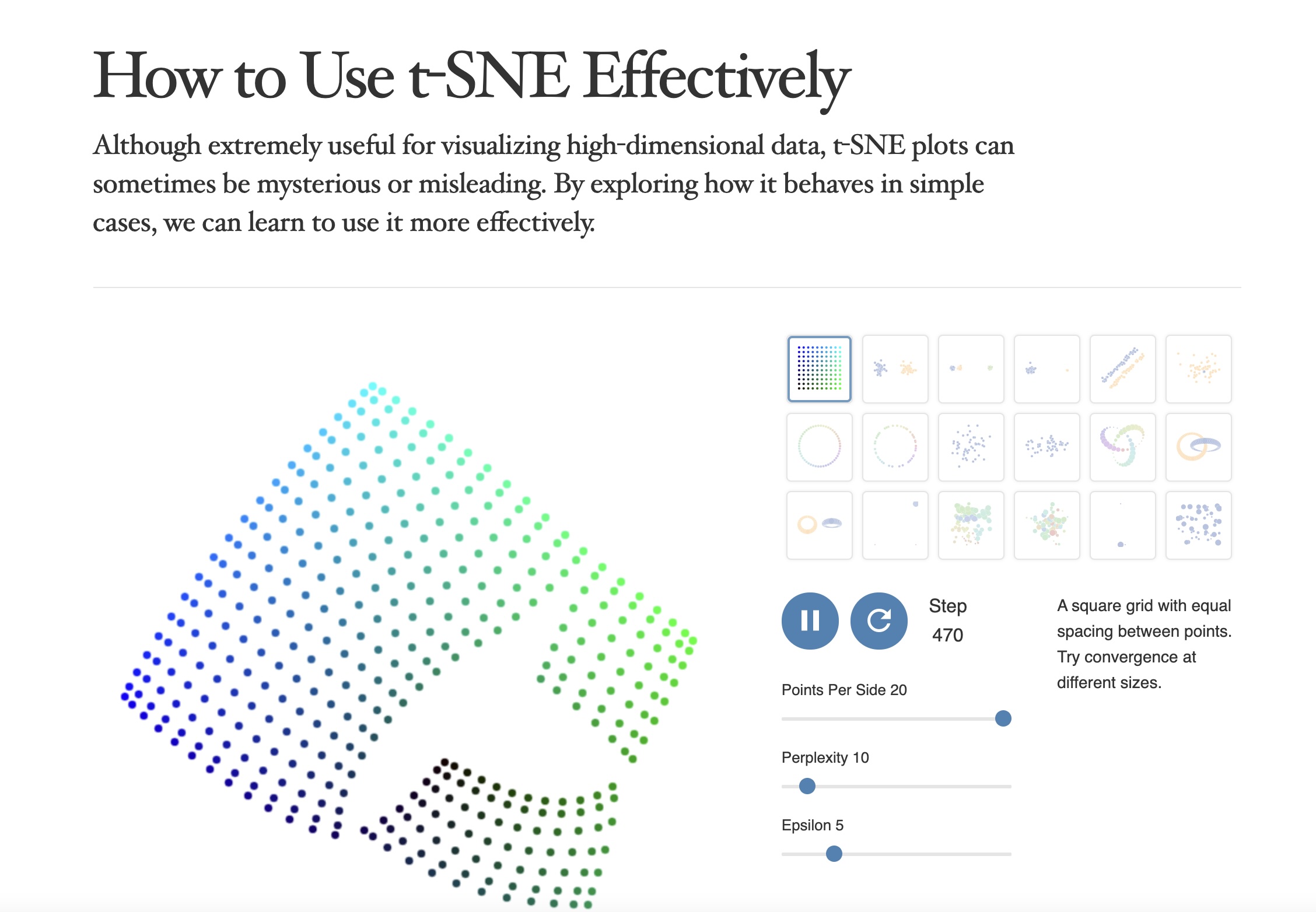 https://distill.pub/2016/misread-tsne/ ##  https://pair-code.github.io/understanding-umap/ ## What about user interaction?