Visualization for Machine Learning

Spring 2024

Deep Learning

• We will start by reviewing concepts of Deep Learning.

Deep Learning

Understanding Deep Learning by Simon J.D. Prince. Published by MIT Press, 2023.

https://udlbook.github.io/udlbook

Deep Learning Terminology

• Inference: \(y = f[x, \Phi]\)

• \(y\): prediction

• \(x\): input

• \(\Phi\): model parameters

• We “learn” the parameters from pairs of “training data” \(\{x_i, y_i\}\)

• We quantify the accuracy by using a (scalar) loss function \(L[\Phi]\). The smaller the loss, the better our model “fits” the data.

• To check the “generalization” of the model, we run the model on “test data”, which is separate from the training data.

1-D linear regression model

• \(y = f[x, \Phi] = \Phi_0 + \Phi_1 x\)

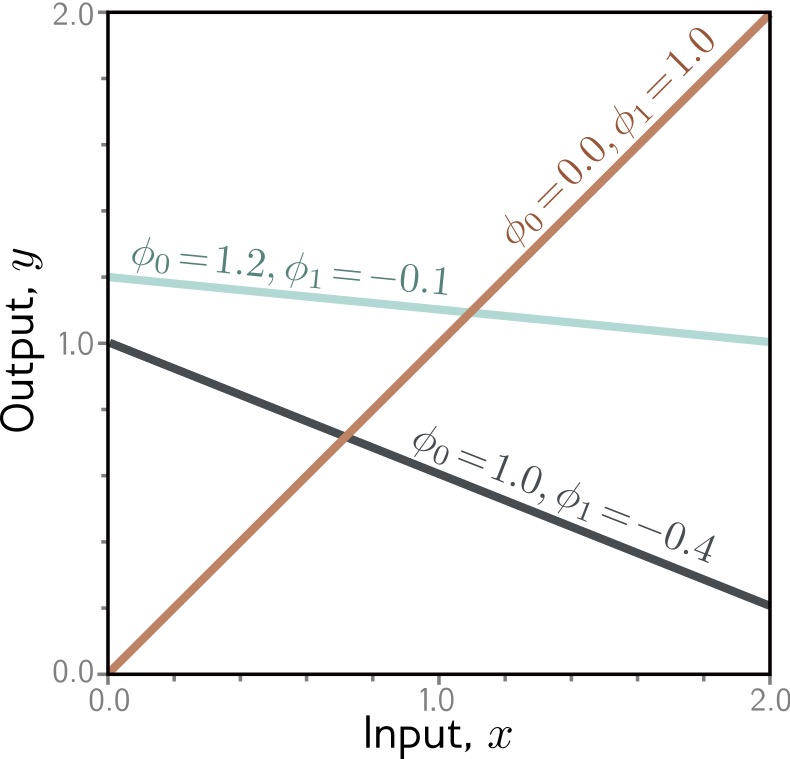
1-D linear regression model: Loss

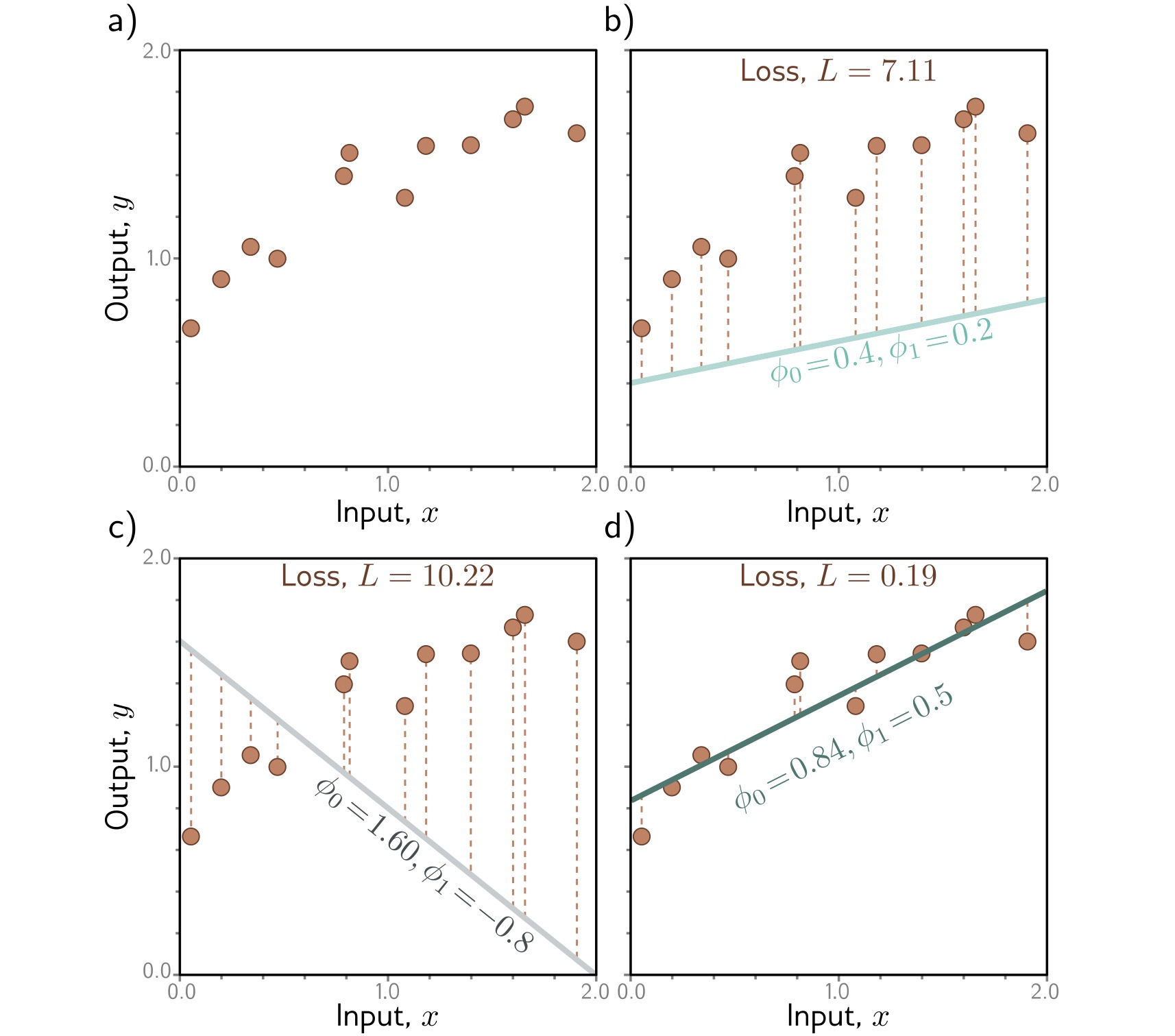
1-D linear regression model: Loss

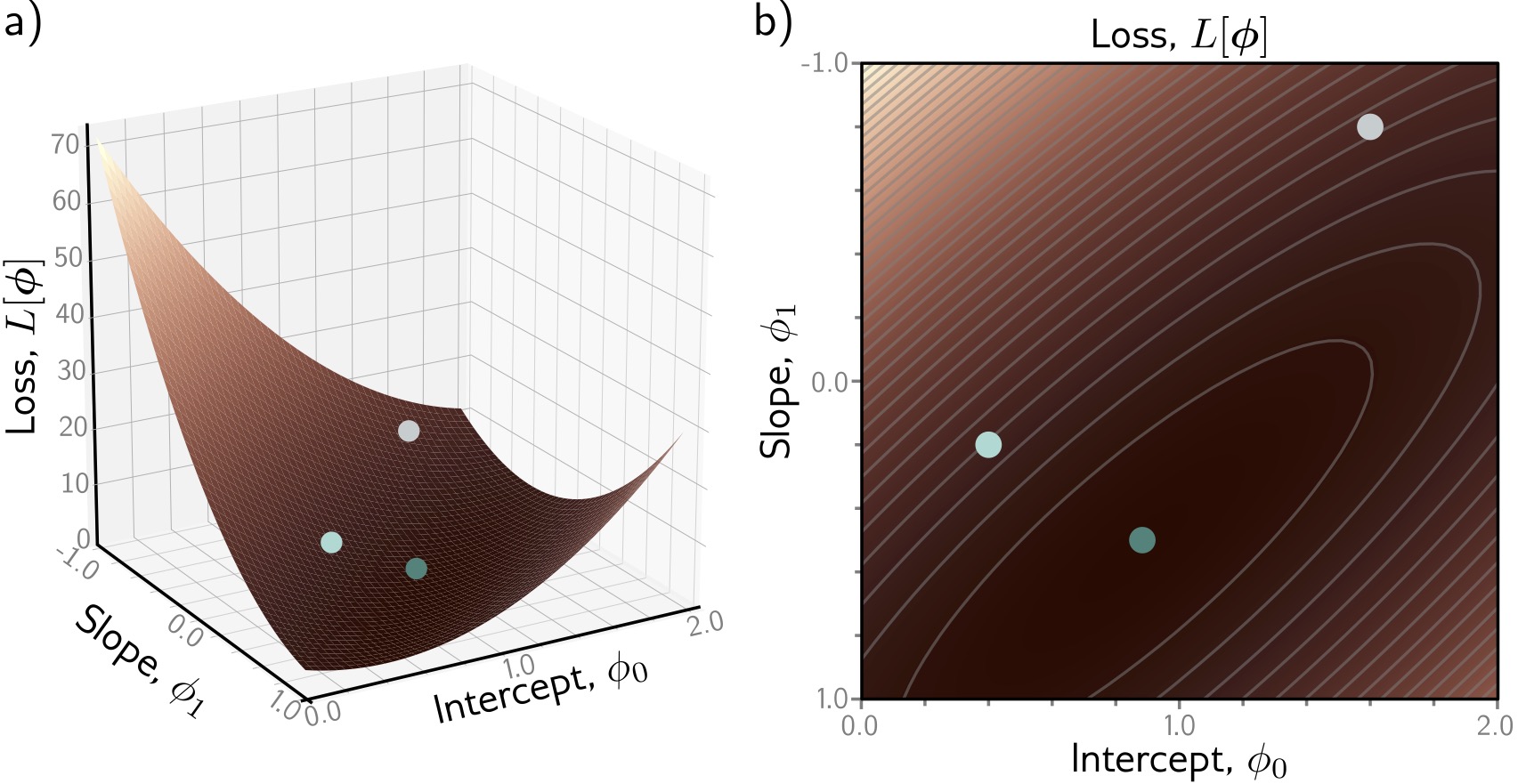
1-D linear regression model: Loss Surface

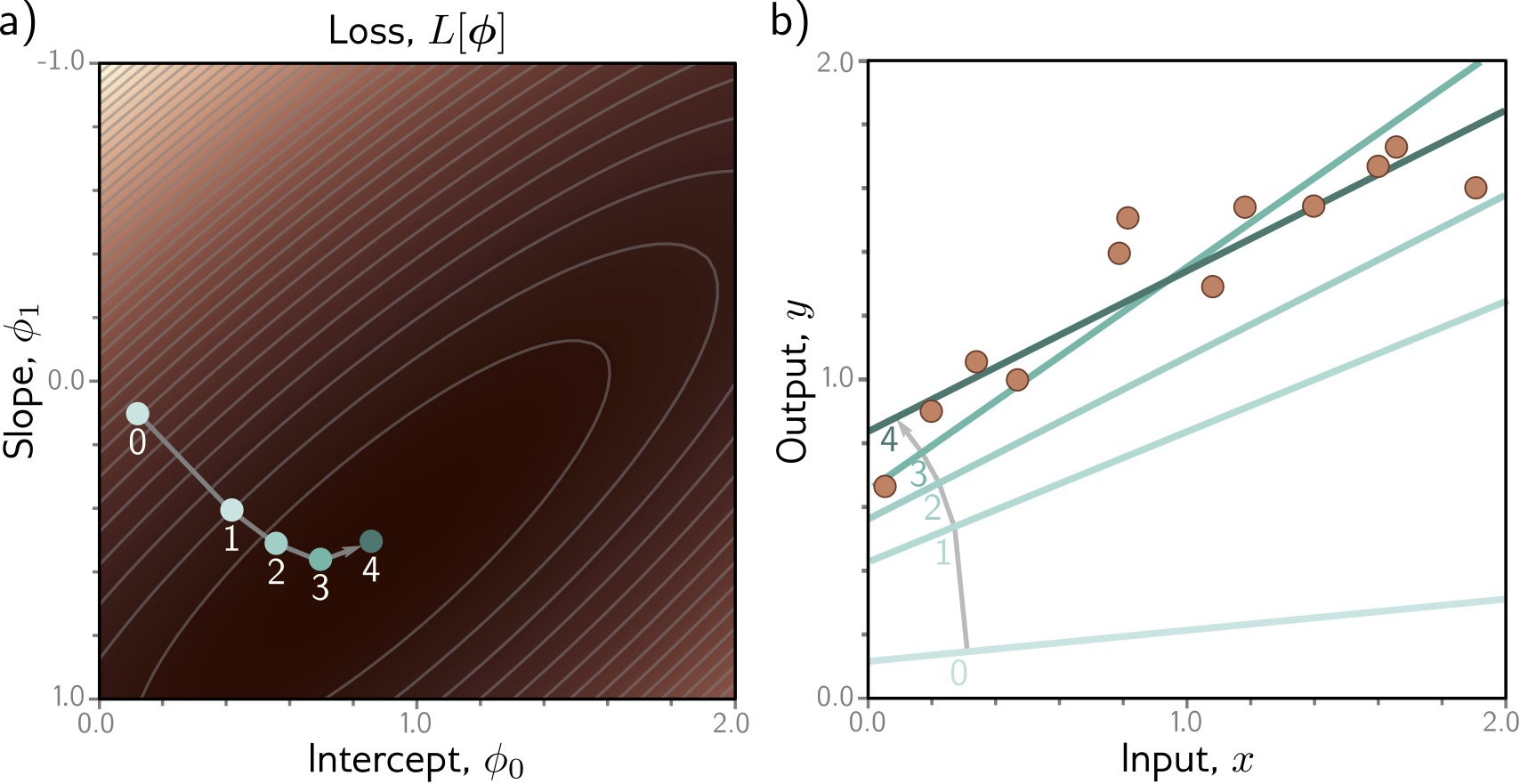
1-D linear regression model: Optimization

Shallow neural networks

• \(y = f[x, \Phi] = \Phi_0 \\ + \Phi_1 a[ \Theta_{10} + \Theta_{11} x] \\ + \Phi_2 a[ \Theta_{20} + \Theta_{21} x] \\ + \Phi_3 a[ \Theta_{30} + \Theta_{31} x]\)

• We now have 10 parameters

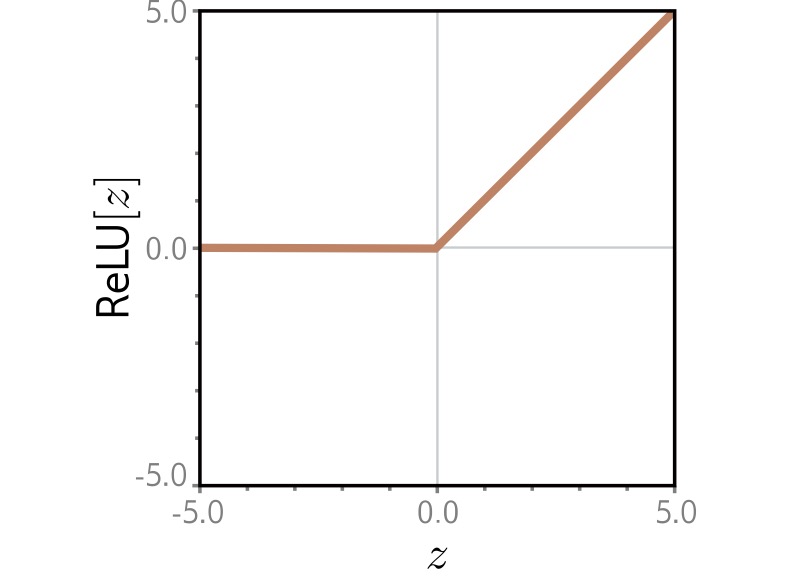
• And also, an “activation” function \(a[]\)

Shallow neural networks: Activation function ReLU

Shallow neural networks: Neural network intuition

Shallow neural networks: Neural network intuition

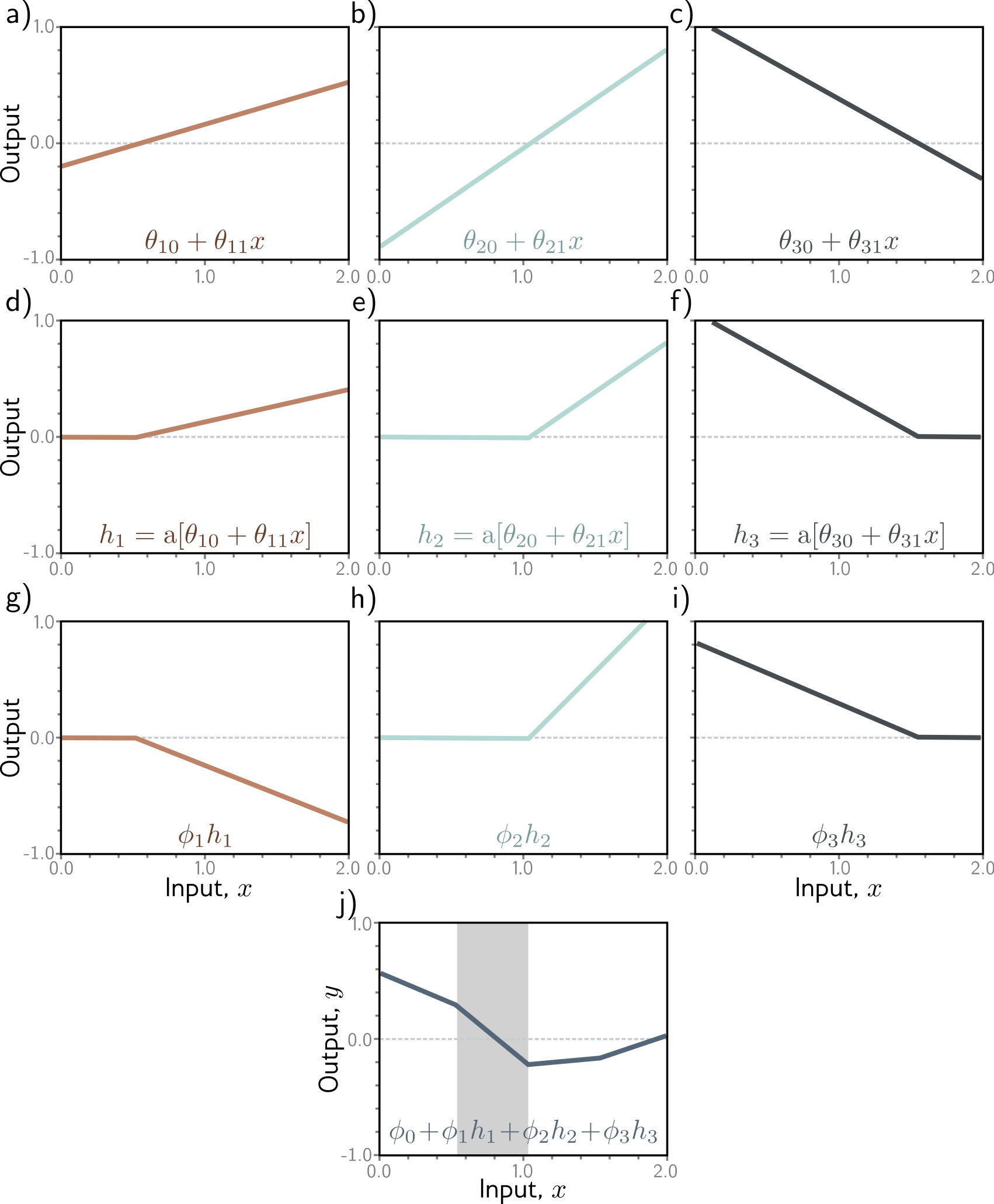
Shallow neural networks: Neural network intuition

Shallow neural networks: Universal Approximation Theorem

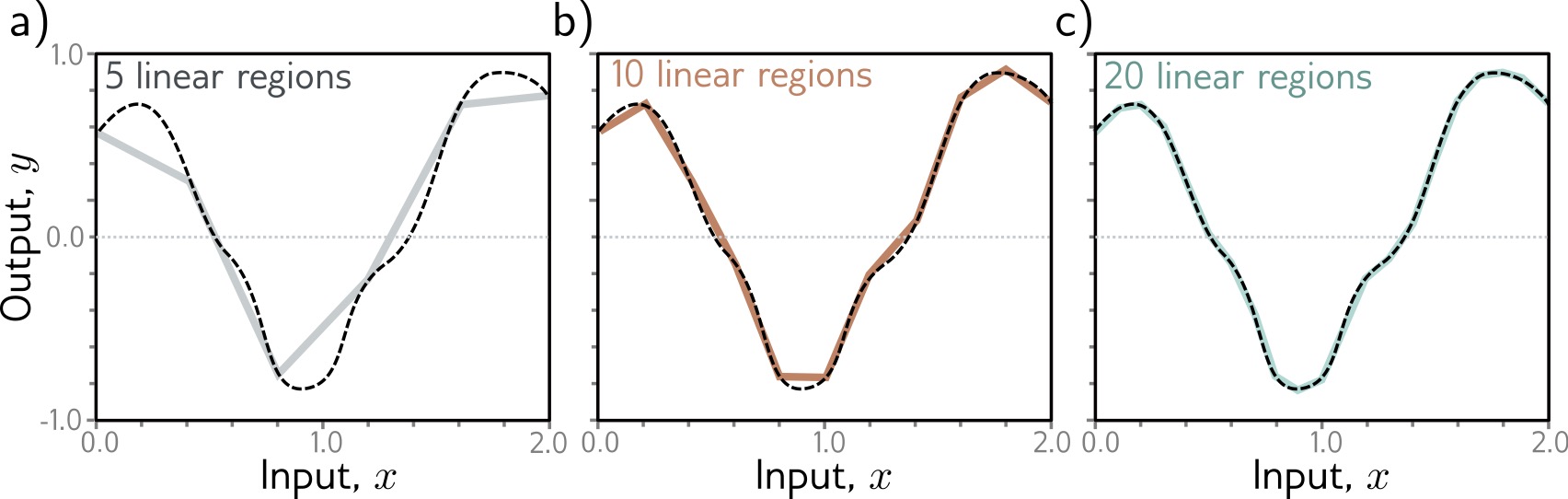
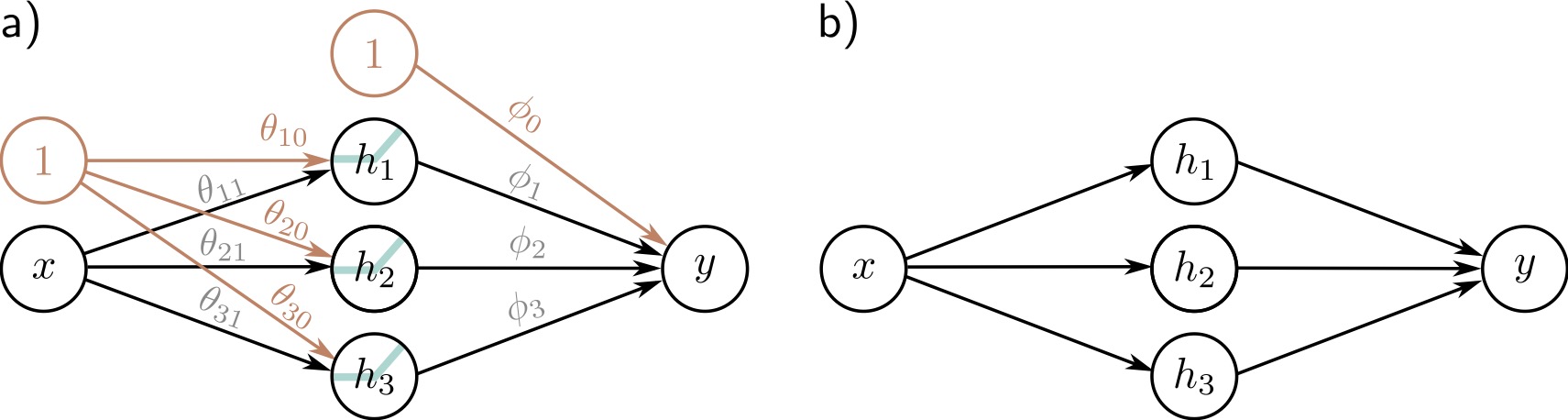
Shallow neural networks: Terminology

• Neural networks is composed of “layers”
• “input” layer, “hidden” layers, “output layer”
• Hidden units are called “neurons”
• As data passes through, the values are called “pre-activation” and “activations”

Deep neural networks: Composing multiple networks

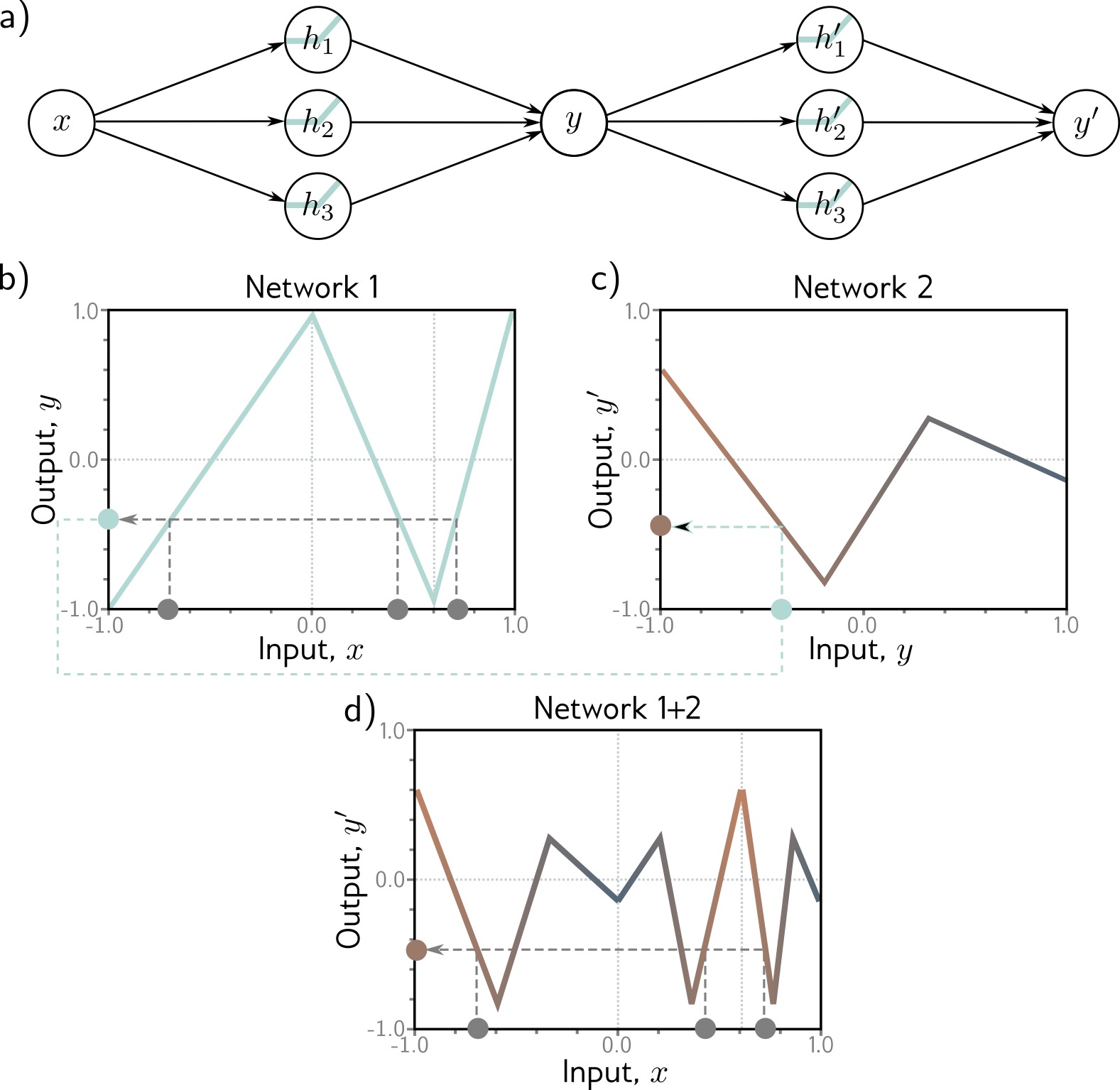
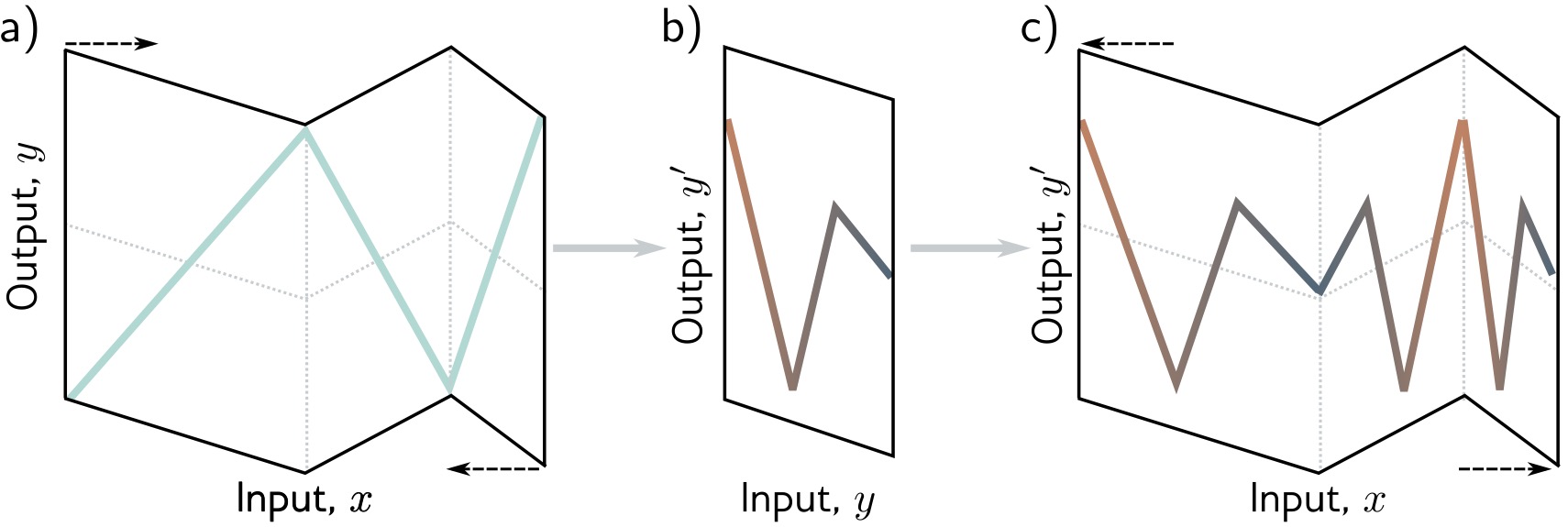
Deep neural networks: Folding Input Space

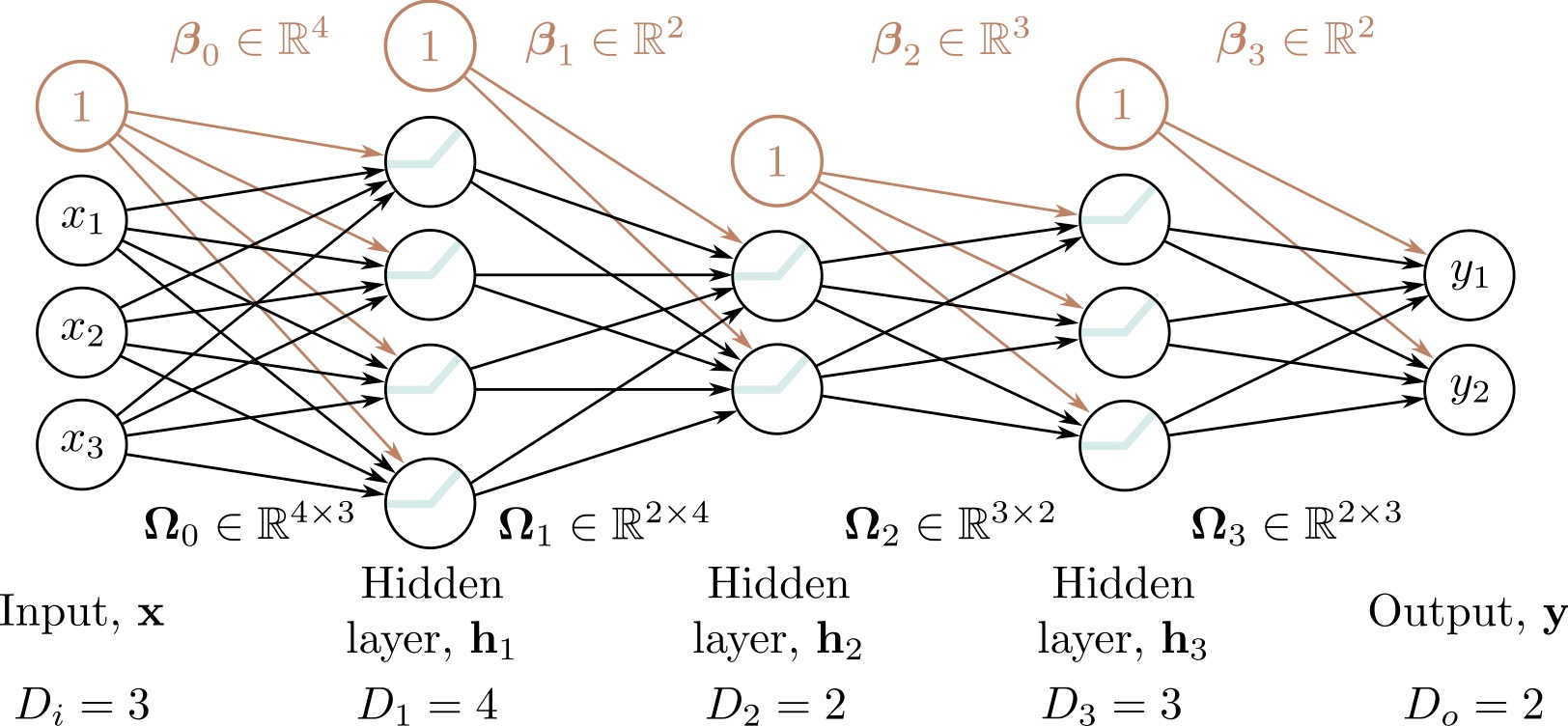
Deep neural networks: Two hidden layers

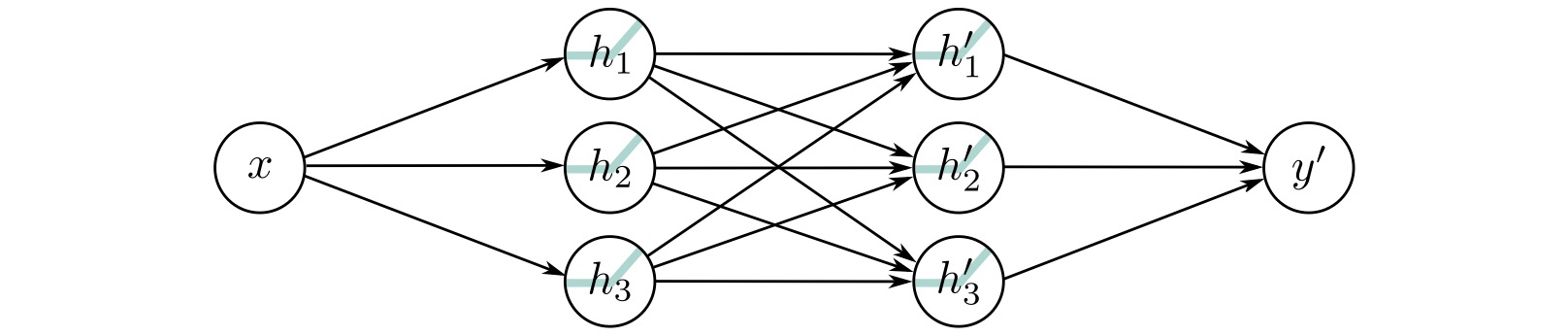
Deep neural networks: Multiple hidden layers

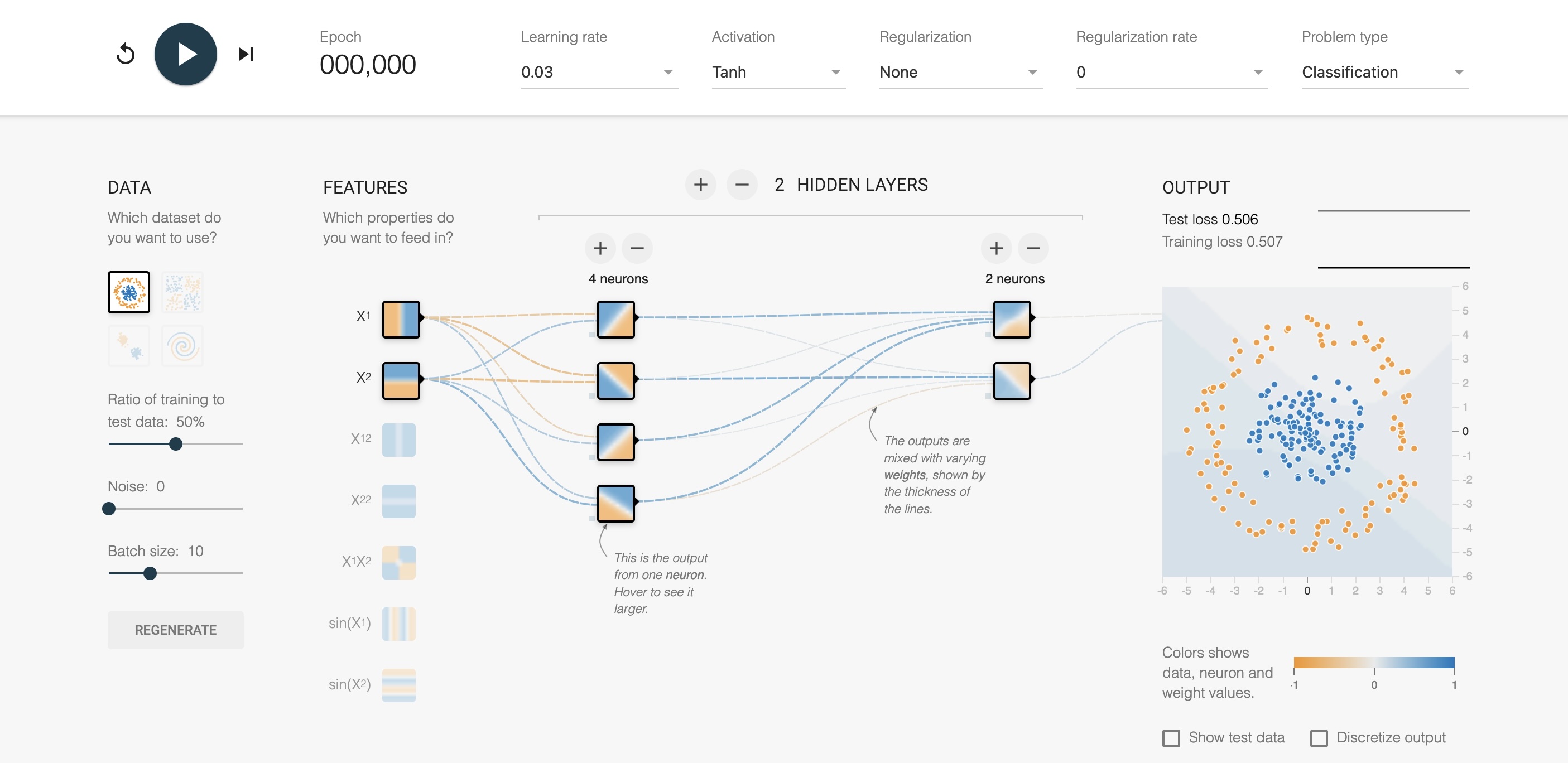
https://playground.tensorflow.org

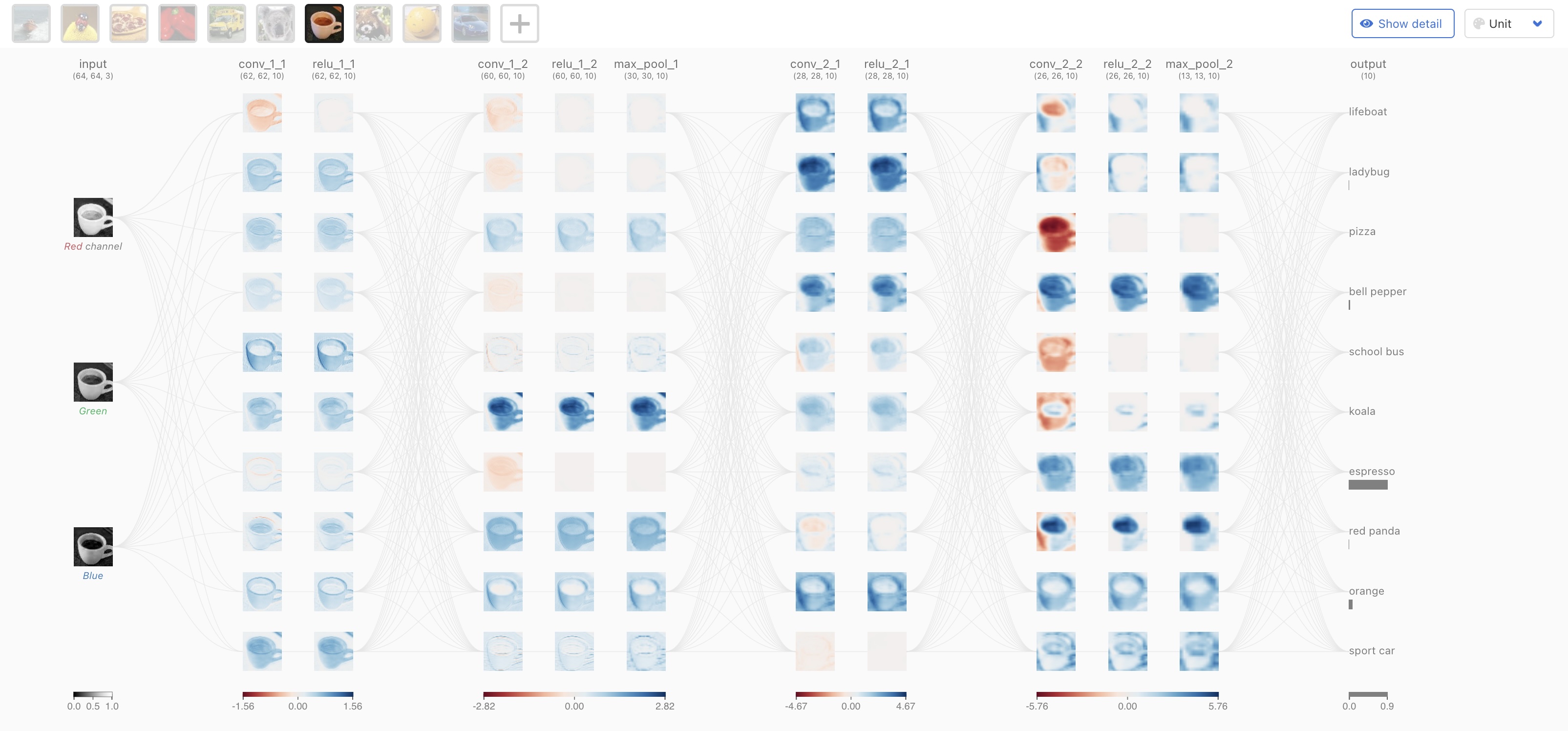
https://poloclub.github.io/cnn-explainer/

Further References

• https://distill.pub/2020/grand-tour/

• http://projector.tensorflow.org/

• https://ml4a.github.io/ml4a/looking_inside_neural_nets/