Visualization for Machine Learning
Spring 2024
Topological Data Analysis
What is topology?
Topology studies the shape of mathematical objects
Unlike Geometry, it is not concerned with sizes, angles, nor coordinates
It is concerned with the connectivity (or lack of) between different “parts” of the object
Two objects are topologically equivalent if we can transform one into another with continuous transformations (without tearing the object)
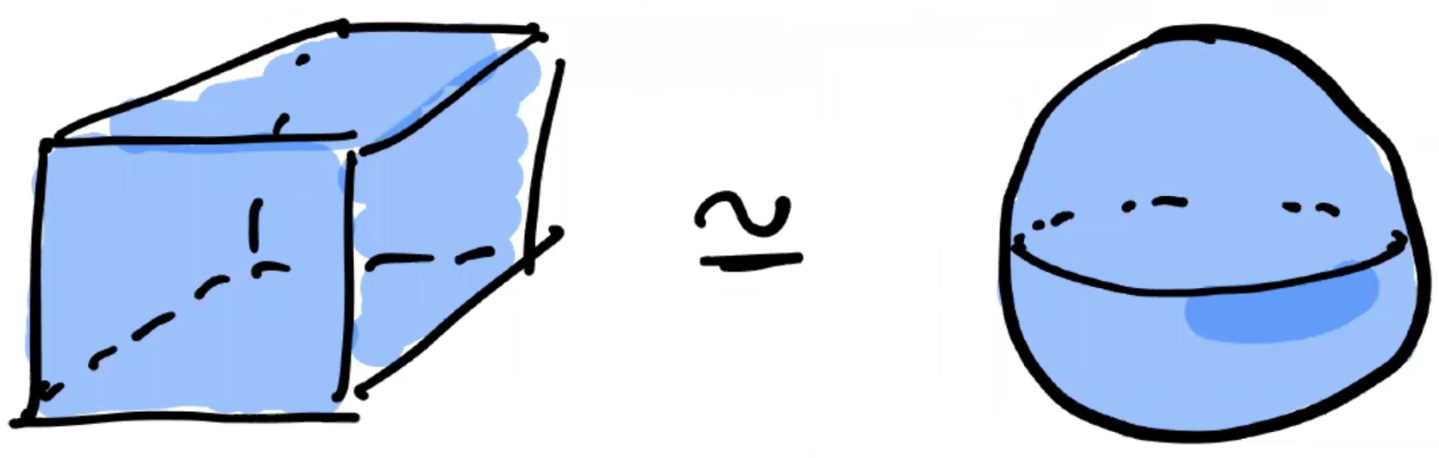
What is topology?

Why topology?
Since topology analyzes the shape while discarding possibly unnecessary information, it is frequently used for analyzing high-dimensional objects
Topological data analysis (TDA) uses techniques from topology to analyze datasets
To do this, it is necessary to construct topological representations of the dataset’s points
Why topology? - An example in chemistry
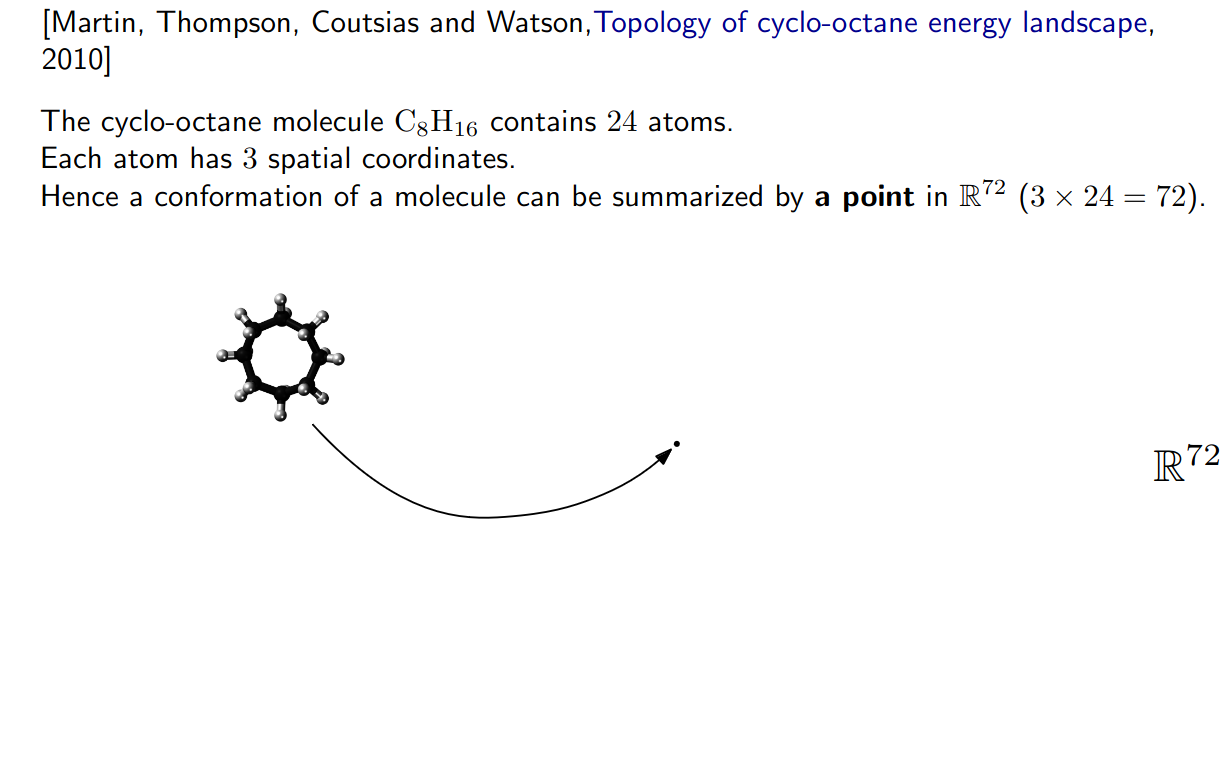
Slides based on Raphaël Tinarrage’s From Algebraic Topology to Data Analysis
Why topology? - An example in chemistry
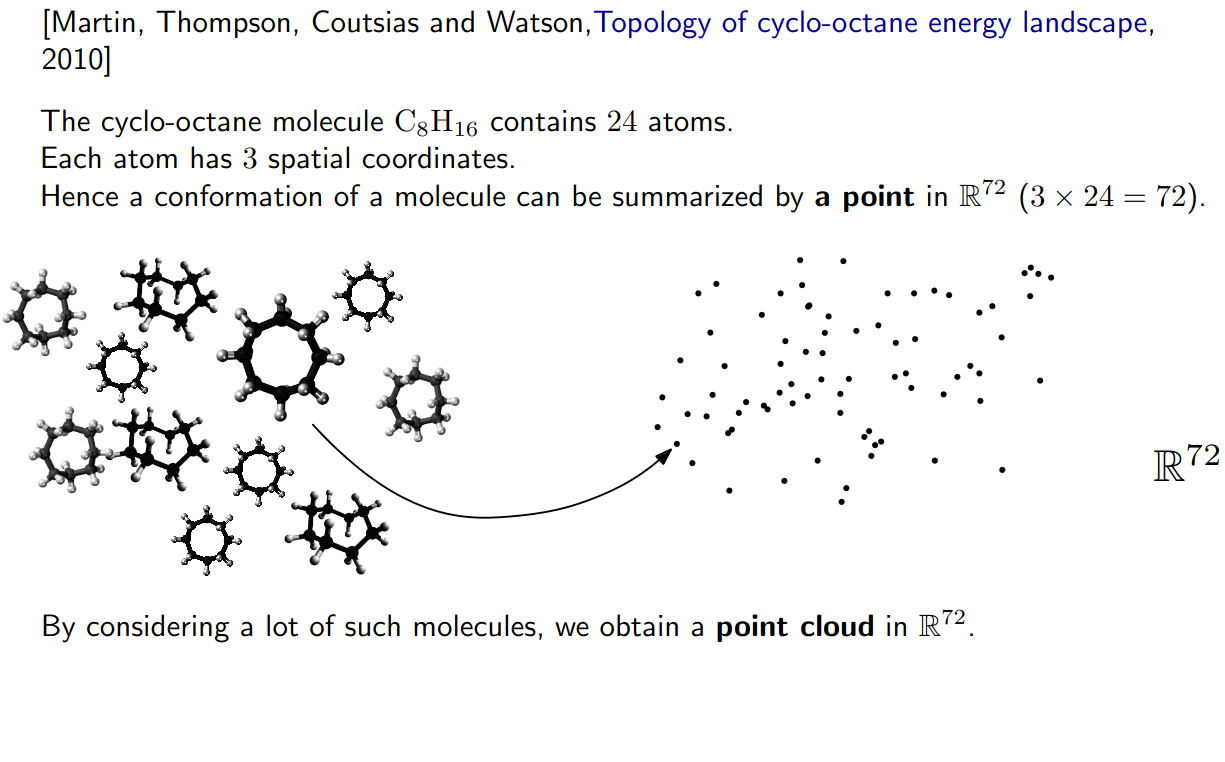
Slides based on Raphaël Tinarrage’s From Algebraic Topology to Data Analysis
Why topology? - An example in chemistry
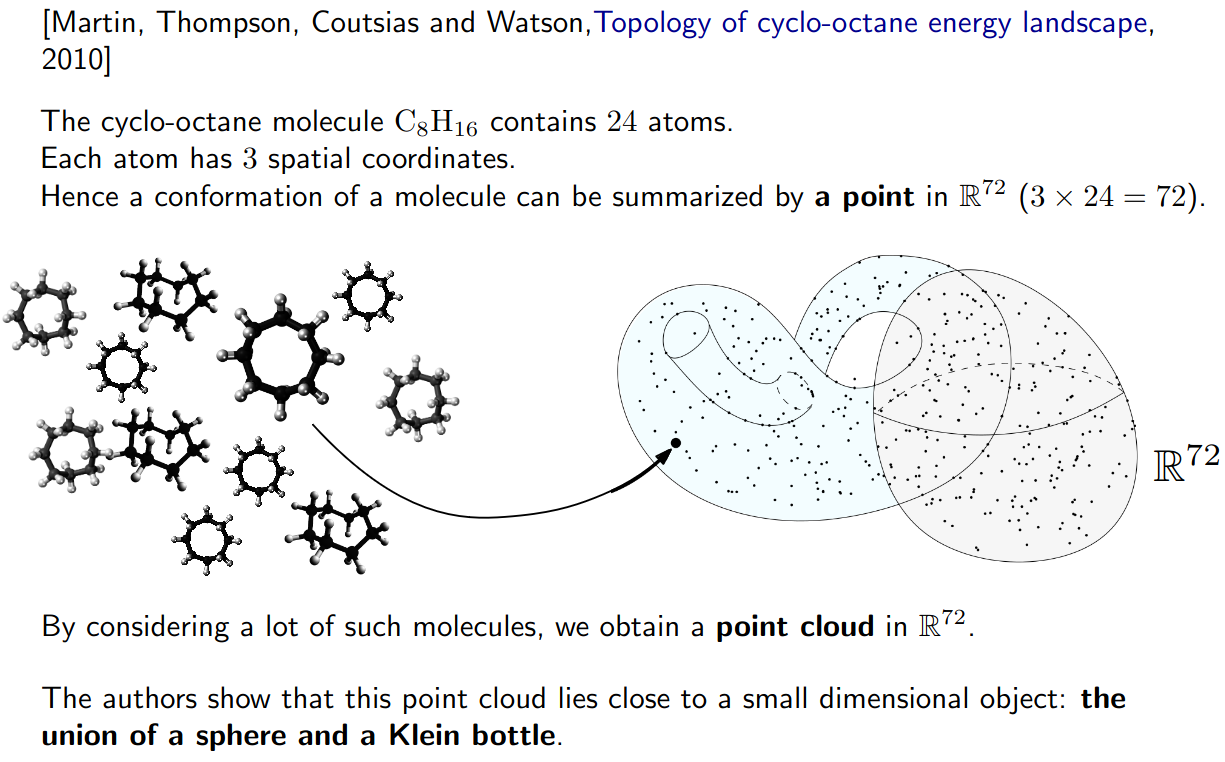
Slides based on Raphaël Tinarrage’s From Algebraic Topology to Data Analysis
Why topology? - An example in biology
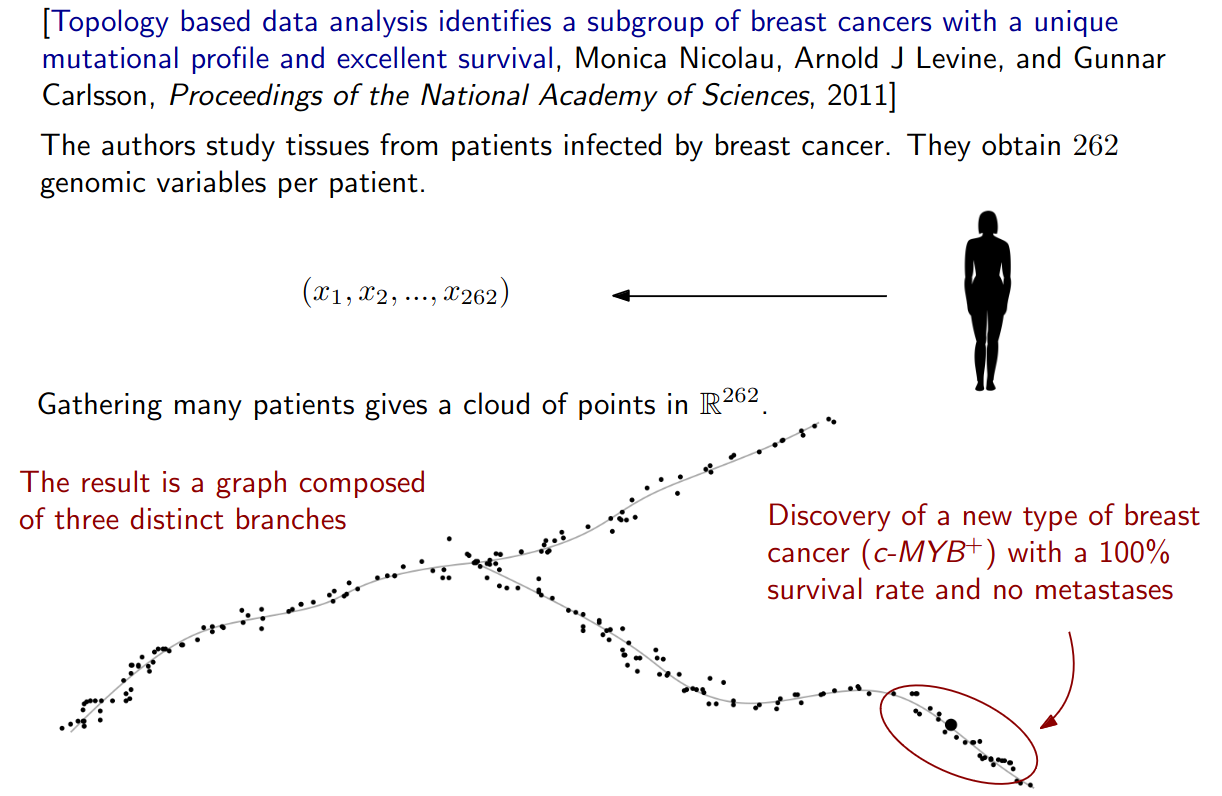
Slides based on Raphaël Tinarrage’s From Algebraic Topology to Data Analysis
Betti numbers
The \(d^{th}\) Betti number counts the number of \(d\)-dimensional holes. It can be used to distinguish between spaces.
\(\beta_0(X)\) Connected components in X
\(\beta_1(X)\) Tunnels or holes in X
\(\beta_2(X)\) Voids in X
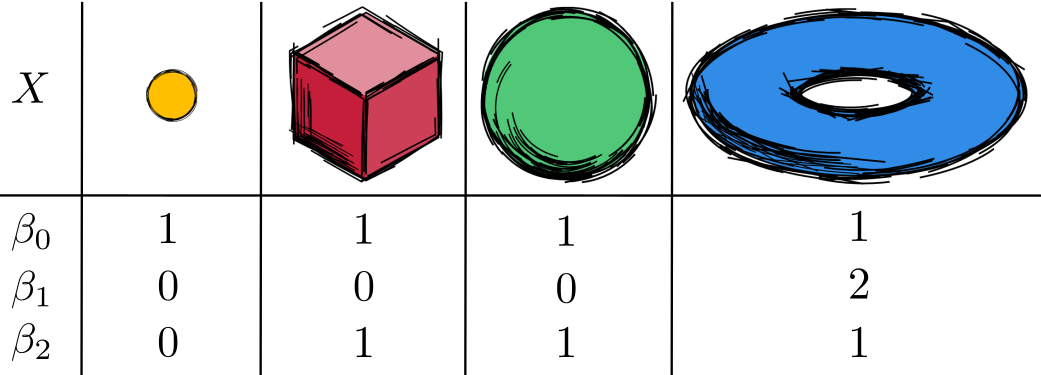
Slides based on Bastian Rieck’s Topological Data Analysis for Machine Learning
First Example - Map
What is a peak?
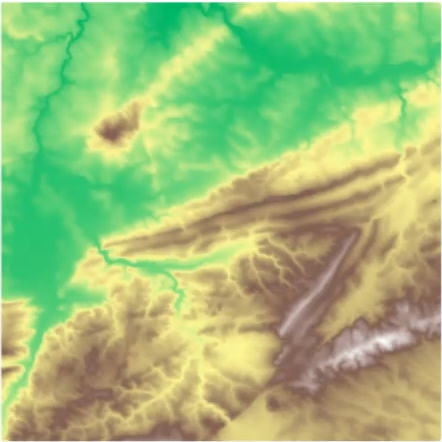
Slides based on Vincent Divol’s CDS Lunch Seminar presentation
First Example - Map
What is a peak?
First idea: Using local maximum

Slides based on Vincent Divol’s CDS Lunch Seminar presentation
First Example - Map
What is a peak?
Second idea: flooding
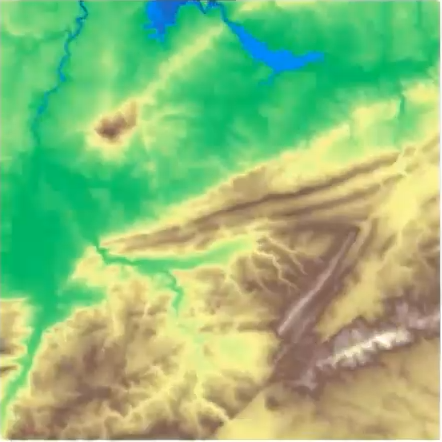
Slides based on Vincent Divol’s CDS Lunch Seminar presentation
First Example - Map
What is a peak?
Second idea: flooding
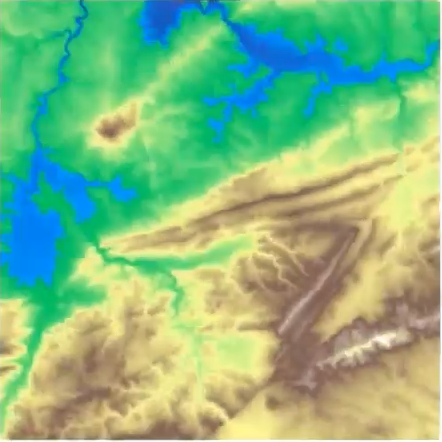
Slides based on Vincent Divol’s CDS Lunch Seminar presentation
First Example - Map
What is a peak?
Second idea: flooding

Slides based on Vincent Divol’s CDS Lunch Seminar presentation
First Example - Map
What is a peak?
Second idea: flooding

Slides based on Vincent Divol’s CDS Lunch Seminar presentation
First Example - Map
What is a peak?
Second idea: flooding

Slides based on Vincent Divol’s CDS Lunch Seminar presentation
First Example - Map
What is a peak?
Second idea: flooding

Slides based on Vincent Divol’s CDS Lunch Seminar presentation
First Example - Map
What is a peak?
Second idea: flooding

Slides based on Vincent Divol’s CDS Lunch Seminar presentation
First Example - Map
The island \(I\) appears at sea level \(b\) (its birth time)…
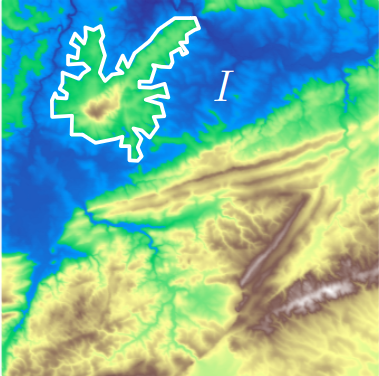
Slides based on Vincent Divol’s CDS Lunch Seminar presentation
First Example - Map
The island \(I\) appears at sea level \(b\) (its birth time)…
and disapears at seas level \(d\) (its death time) at local maximum \(x\).
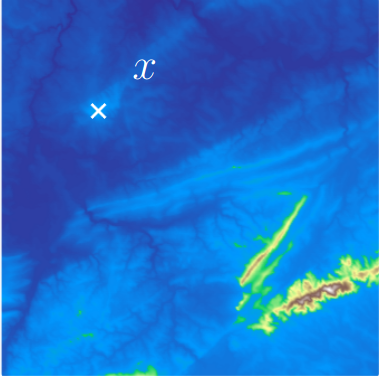
The point \(x\) is a peak if the persistence\(:= d-b\) of the island \(I\) is larger than \(91\)m (=\(300\)ft).
Slides based on Vincent Divol’s CDS Lunch Seminar presentation
First Example - Map

The persistence diagram (PD) of the elevation function is the collection of the points \((b,d)\), where \((b,d)\) corresponds to the birth/death of an island.
Slides based on Vincent Divol’s CDS Lunch Seminar presentation
First Example - Map
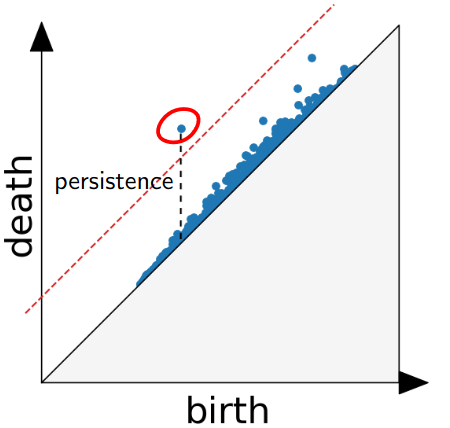
The persistence diagram (PD) of the elevation function is the collection of the points \((b,d)\), where \((b,d)\) corresponds to the birth/death of an island.
Slides based on Vincent Divol’s CDS Lunch Seminar presentation
Second Example
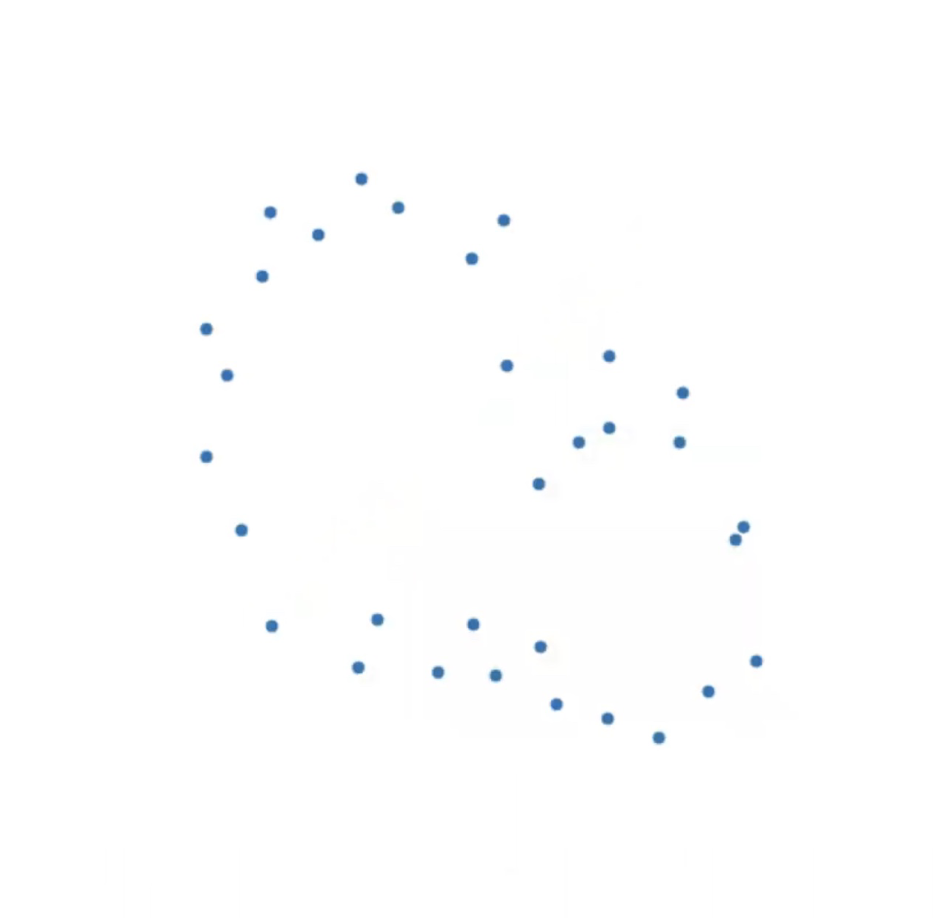
Slides based on Vincent Divol’s CDS Lunch Seminar presentation
Second Example

Slides based on Vincent Divol’s CDS Lunch Seminar presentation
Second Example

Slides based on Vincent Divol’s CDS Lunch Seminar presentation
Second Example

Slides based on Vincent Divol’s CDS Lunch Seminar presentation
Second Example

Slides based on Vincent Divol’s CDS Lunch Seminar presentation
Second Example

Slides based on Vincent Divol’s CDS Lunch Seminar presentation
Second Example

Slides based on Vincent Divol’s CDS Lunch Seminar presentation
Second Example

Slides based on Vincent Divol’s CDS Lunch Seminar presentation
Second Example

Slides based on Vincent Divol’s CDS Lunch Seminar presentation
Second Example

Slides based on Vincent Divol’s CDS Lunch Seminar presentation
Second Example

Slides based on Vincent Divol’s CDS Lunch Seminar presentation
Second Example

Slides based on Vincent Divol’s CDS Lunch Seminar presentation
Second Example
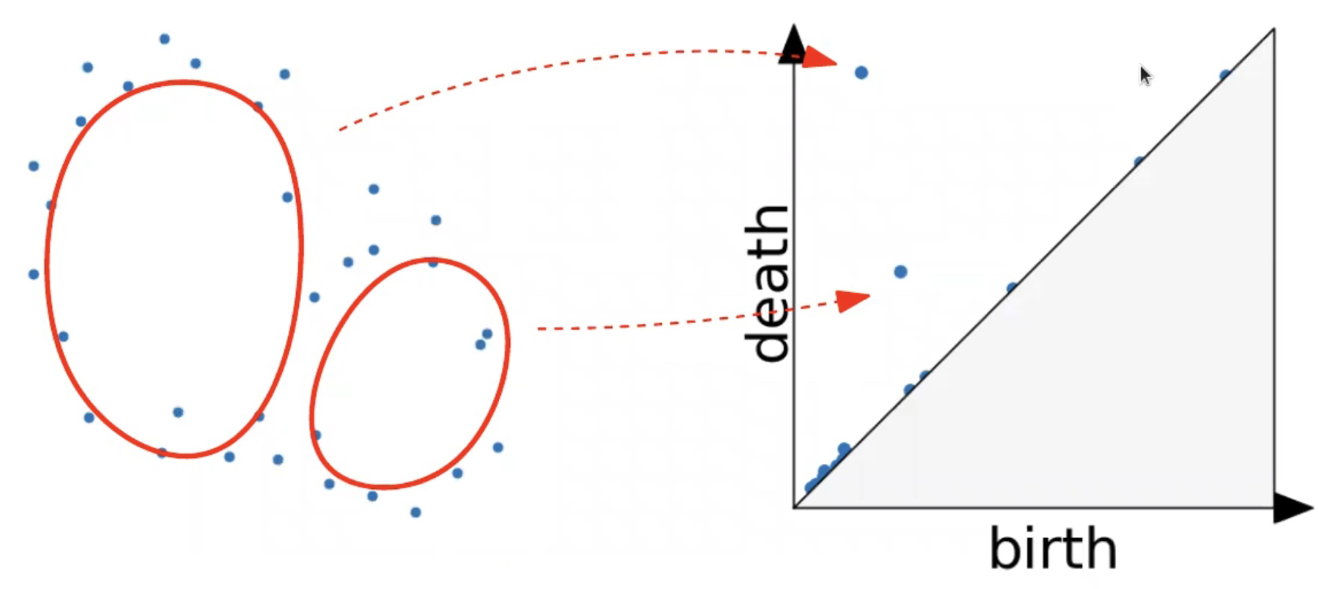
Slides based on Vincent Divol’s CDS Lunch Seminar presentation
Persistence diagram
Slides based on Vincent Divol’s CDS Lunch Seminar presentation
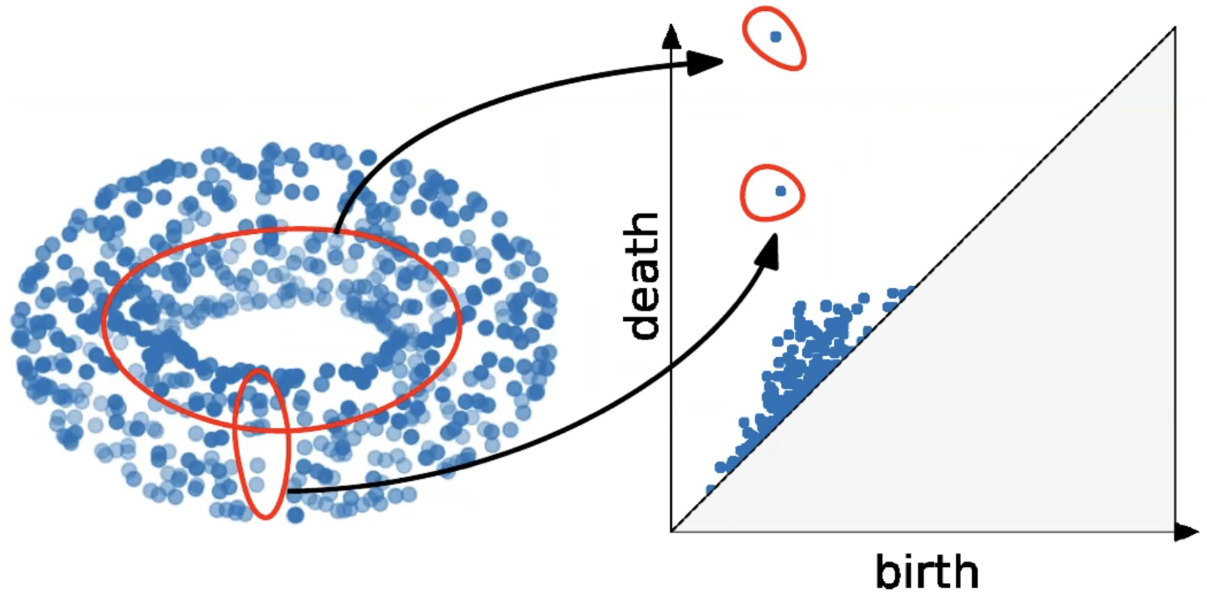
Distance between persistence diagrams
If we have more than one persistence diagram, how do we measure the distance between them?
Slides based on Vincent Divol’s CDS Lunch Seminar presentation
Distance between persistence diagrams
We place both in the same diagram
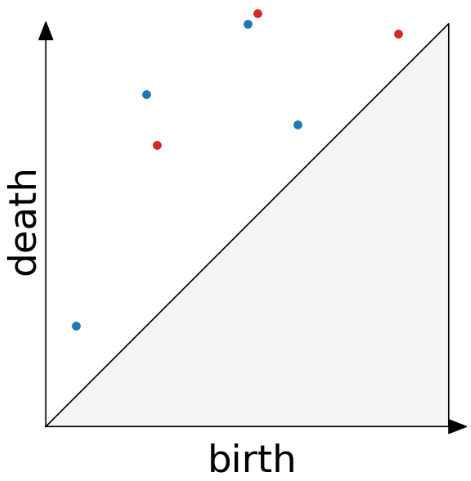
Slides based on Vincent Divol’s CDS Lunch Seminar presentation
Distance between persistence diagrams
We place both in the same diagram
Get the optimal pair matching between the points (including the diagonal)
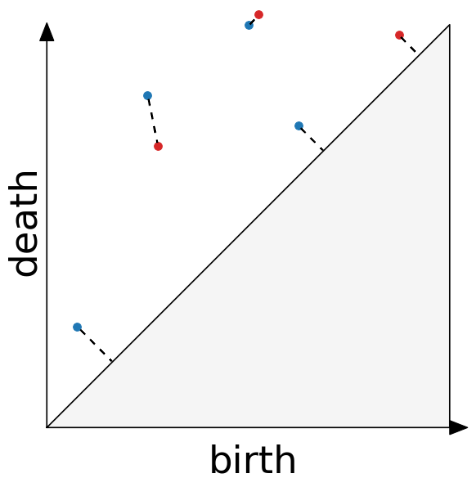
Slides based on Vincent Divol’s CDS Lunch Seminar presentation
Distance between persistence diagrams
We place both in the same diagram
Get the optimal pair matching between the points (including the diagonal)
The bottleneck distance between them will be the largest pair distance

Slides based on Vincent Divol’s CDS Lunch Seminar presentation
Simplicial complexes
Definition
We call a non-empty family of sets \(K\) with a collection of non-empty subsets \(S\) an abstract simplicial complex if:
- \(\{v\} \in S\) for all \(v \in K\)
- If \(\sigma \in S\) and \(\tau \subseteq \sigma\), then \(\tau \in K\).
Terminology
The elements of a simplicial complex \(K\) are called simplices. A \(k\)-simplex consists of \(k+1\) verticies.
Slides based on Bastian Rieck’s Topological Data Analysis for Machine Learning
Simplicial complexes
Example
Simplicial complexes can be decomposed into their skeletons, which only contain simplices of a certain dimension.

Slides based on Bastian Rieck’s Topological Data Analysis for Machine Learning
Simplicial complexes
Example
Simplicial complexes can be decomposed into their skeletons, which only contain simplices of a certain dimension.
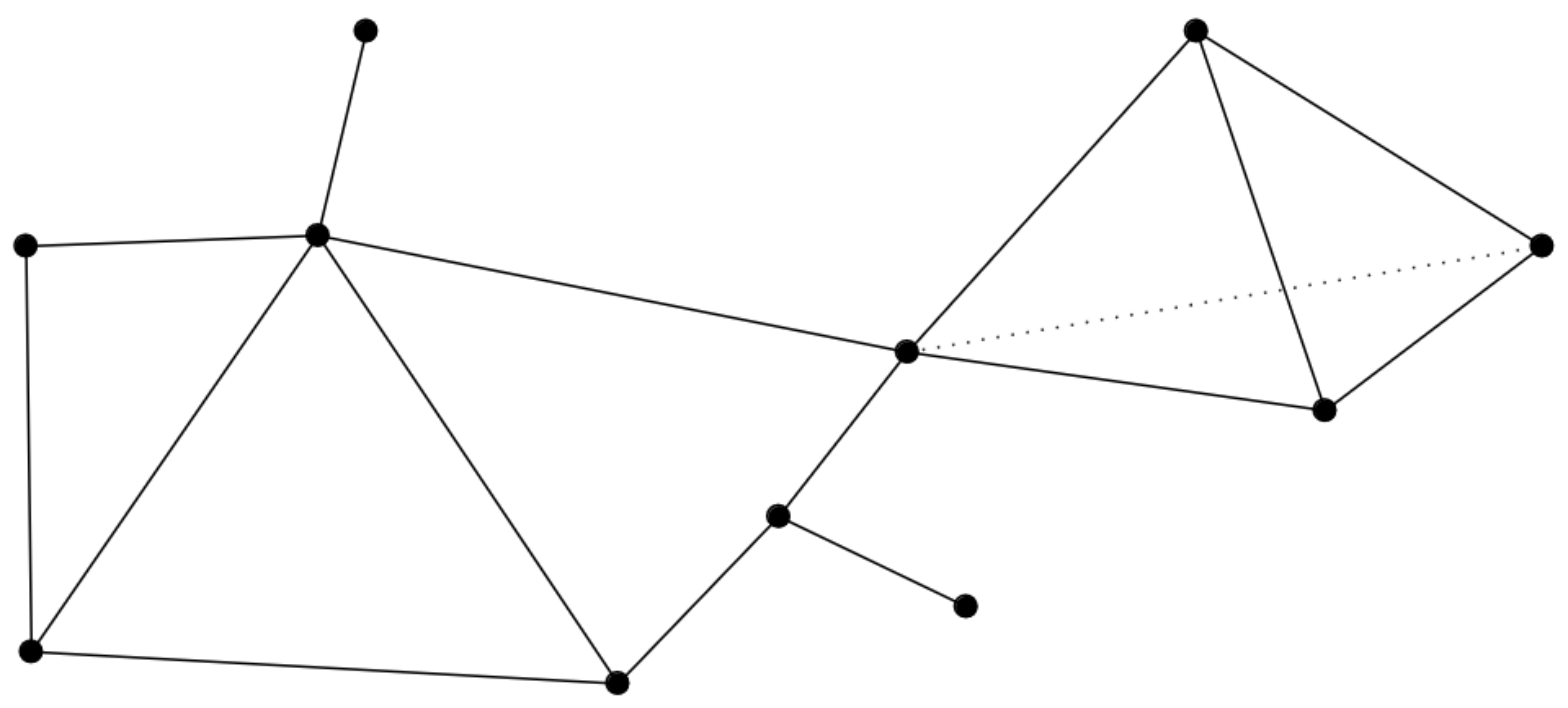
Slides based on Bastian Rieck’s Topological Data Analysis for Machine Learning
Simplicial complexes
Example
Simplicial complexes can be decomposed into their skeletons, which only contain simplices of a certain dimension.
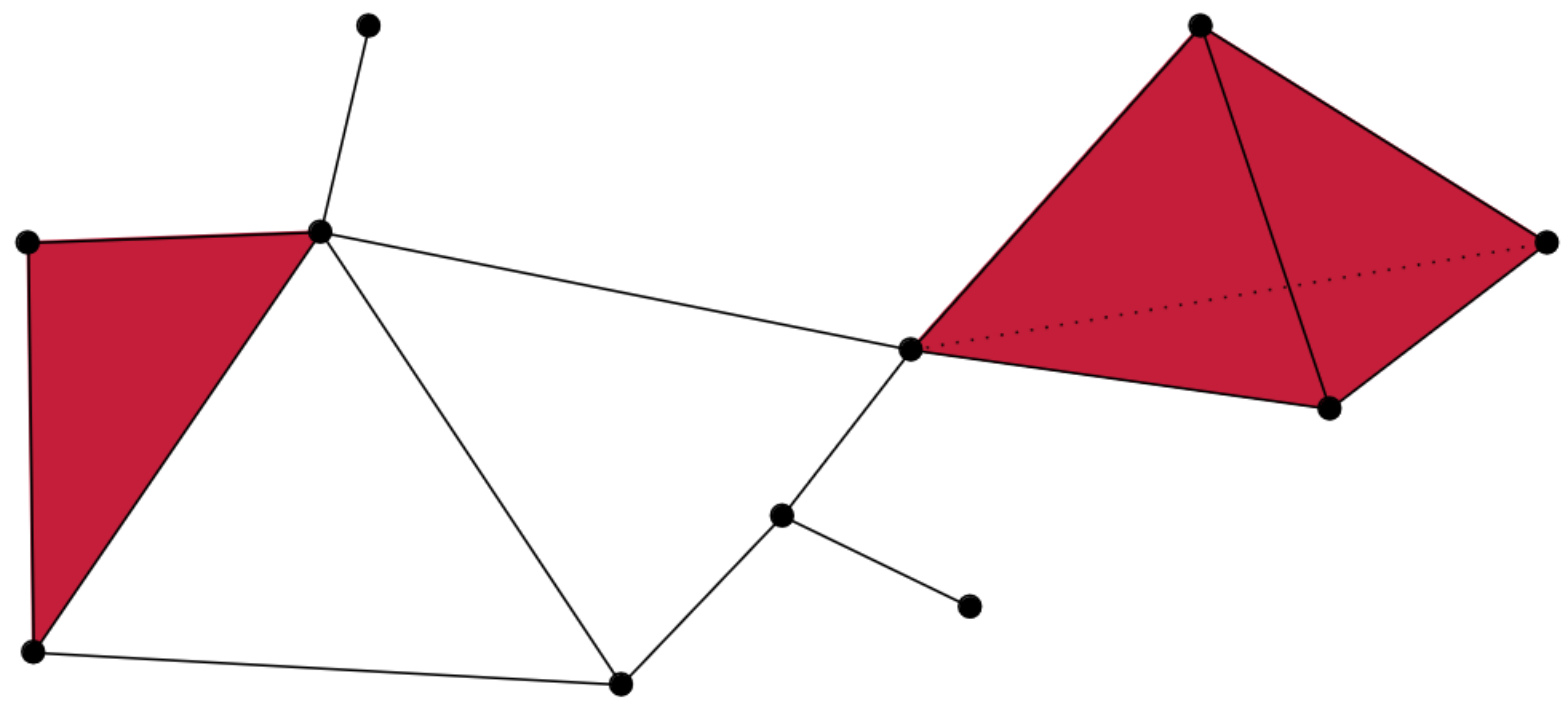
Slides based on Bastian Rieck’s Topological Data Analysis for Machine Learning
Simplicial complexes
Example
Simplicial complexes can be decomposed into their skeletons, which only contain simplices of a certain dimension.
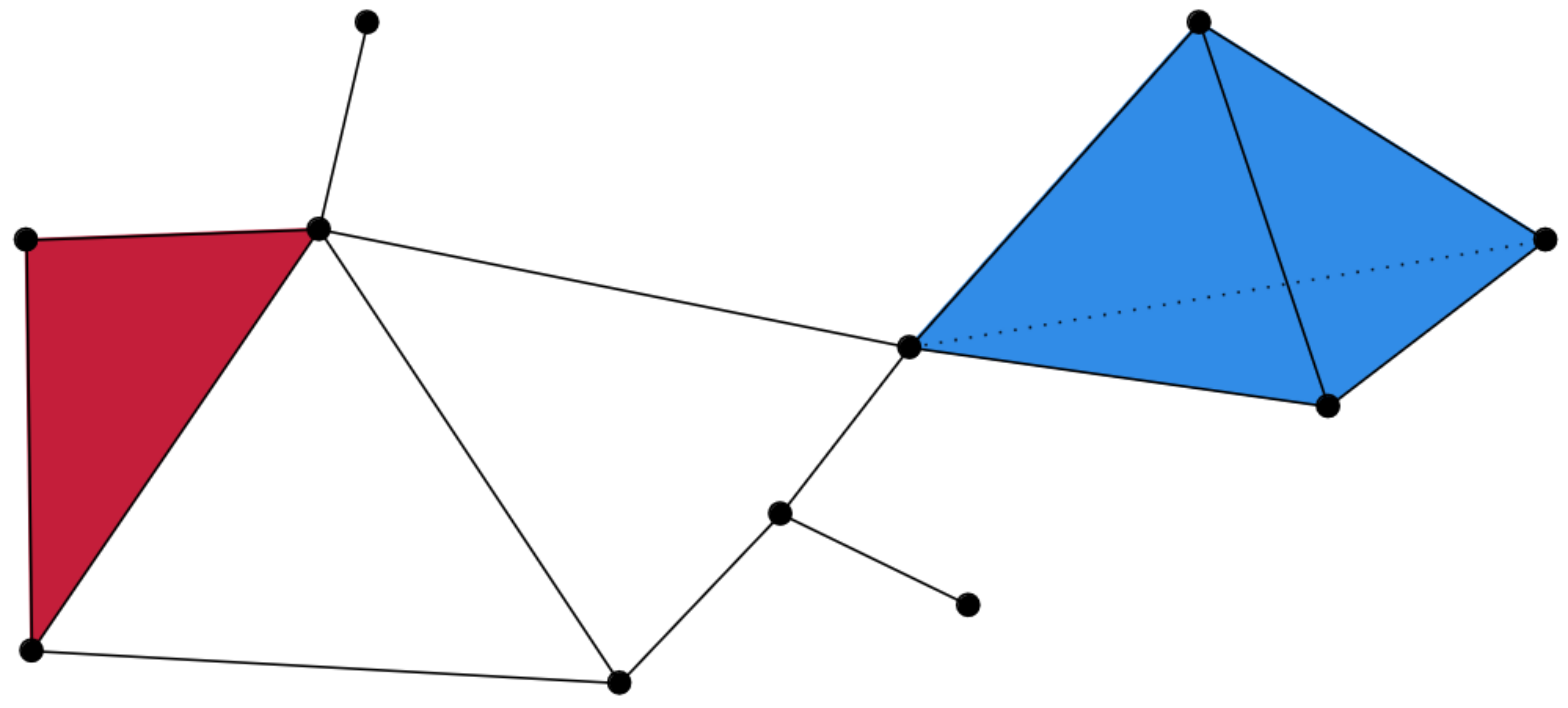
Slides based on Bastian Rieck’s Topological Data Analysis for Machine Learning
Simplicial complexes
Non-example
This is not a simplicial complex because some higher-dimensional simplices do not intersect in a lower dimensional one!
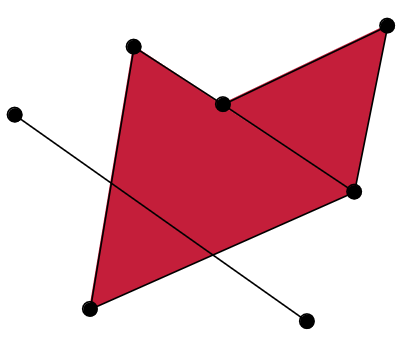
Slides based on Bastian Rieck’s Topological Data Analysis for Machine Learning
Simplicial complexes
Example

Notice that \(K\) does not contain the 2-simplex \(\{a,b,c\}\)
Slides based on Bastian Rieck’s Topological Data Analysis for Machine Learning
From points clouds to simplicial complexes
From points clouds to simplicial complexes

From points clouds to simplicial complexes

Strategy 1: Triangulation
Constructing the data’s simplicial complex
Vietoris-Rips construction
Definition
Given a set of points \(\mathcal{X} = \{x_1,\dots,x_n\}\) and a metric \(dist\) (such as the Euclidean distance), pick a threshold \(\epsilon\) and build the Vietoris-Rips complex \(\mathcal{V}_\epsilon\) defined as:
\[\mathcal{V}_\epsilon := \{\sigma \subseteq \mathcal{X} | \forall u,v \in \sigma : dist(u,v) \leq \epsilon\}\]
Equivalently, \(\mathcal{V}_\epsilon\) contains all simplices whose diameter is less than or equal to \(\epsilon\).
Slides based on Bastian Rieck’s Topological Data Analysis for Machine Learning
Vietoris-Rips construction
Example
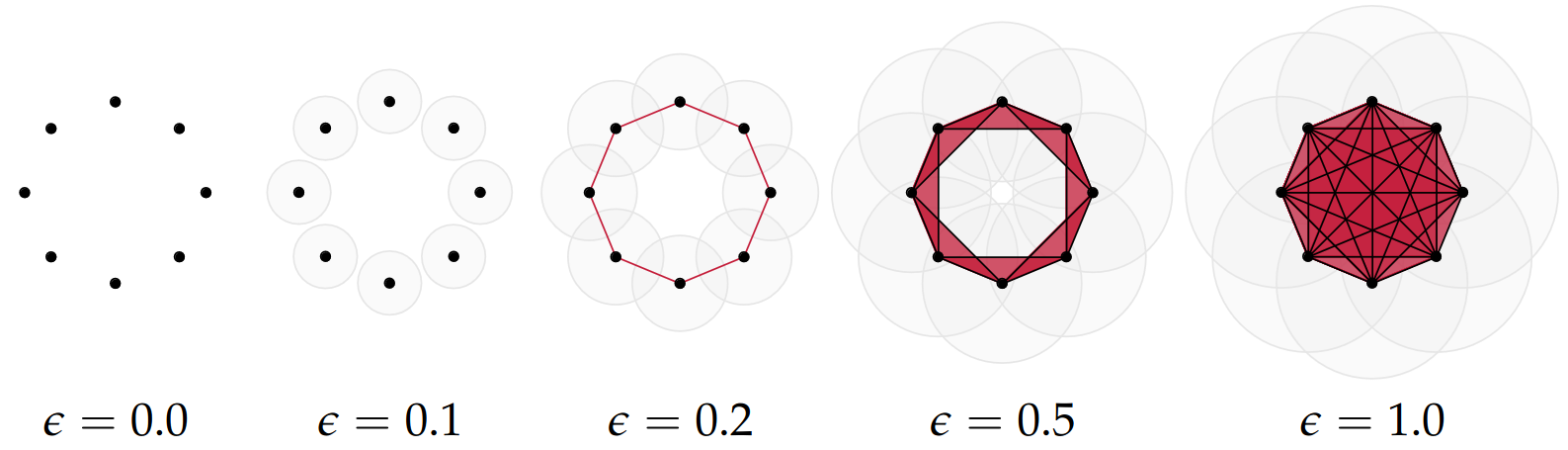
Draw Euclidean balls (circles) of diameter \(\epsilon\) and create a \(k\)-simplex \(\sigma\) for each subset of \(k+1\) points that intersect pairwise.
Slides based on Bastian Rieck’s Topological Data Analysis for Machine Learning
Some details about this construction

This construction dates back to a 1927 article by Leopold Vietoris\(^1\)
A 2010 paper by Afra Zomorodian\(^2\) describes several construction algorithms
The basic idea is to build higher-dimensional simplices inductively from lower-dimensional ones
In the worst case, the Vietoris-Rips complex will contain all \(2^n\) subsets of its underluing point clous \(\mathcal{X}\)!
\(^1\) Vietoris, Leopold. “Über den höheren Zusammenhang kompakter Räume und eine Klasse von zusammenhangstreuen Abbildungen.” Mathematische Annalen 97.1 (1927): 454-472.
\(^2\) Zomorodian, Afra. “Fast construction of the Vietoris-Rips complex.” Computers & Graphics 34.3 (2010): 263-271.
Slides based on Bastian Rieck’s Topological Data Analysis for Machine Learning
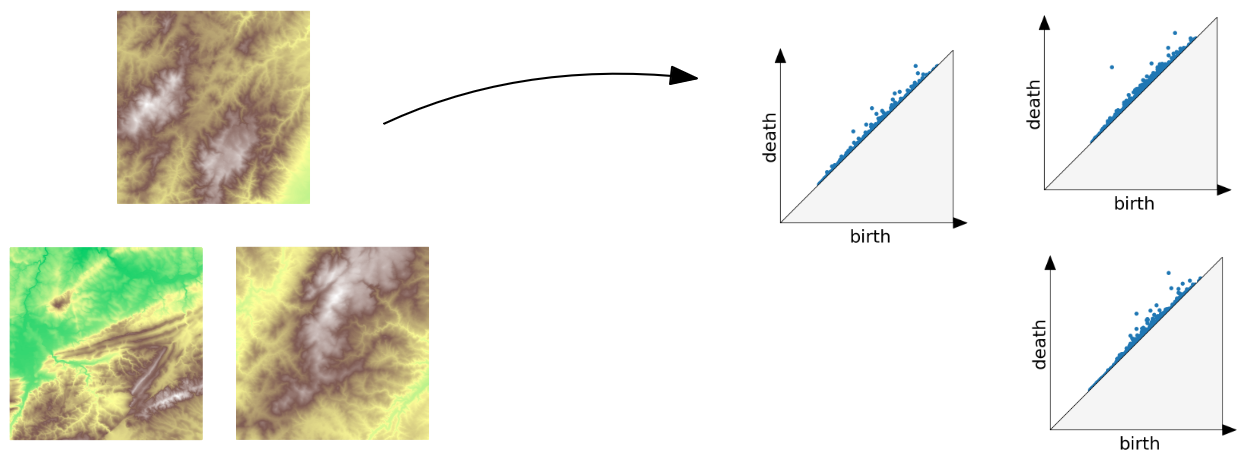
The betti numbers of a Vietoris-Rips complex
Example
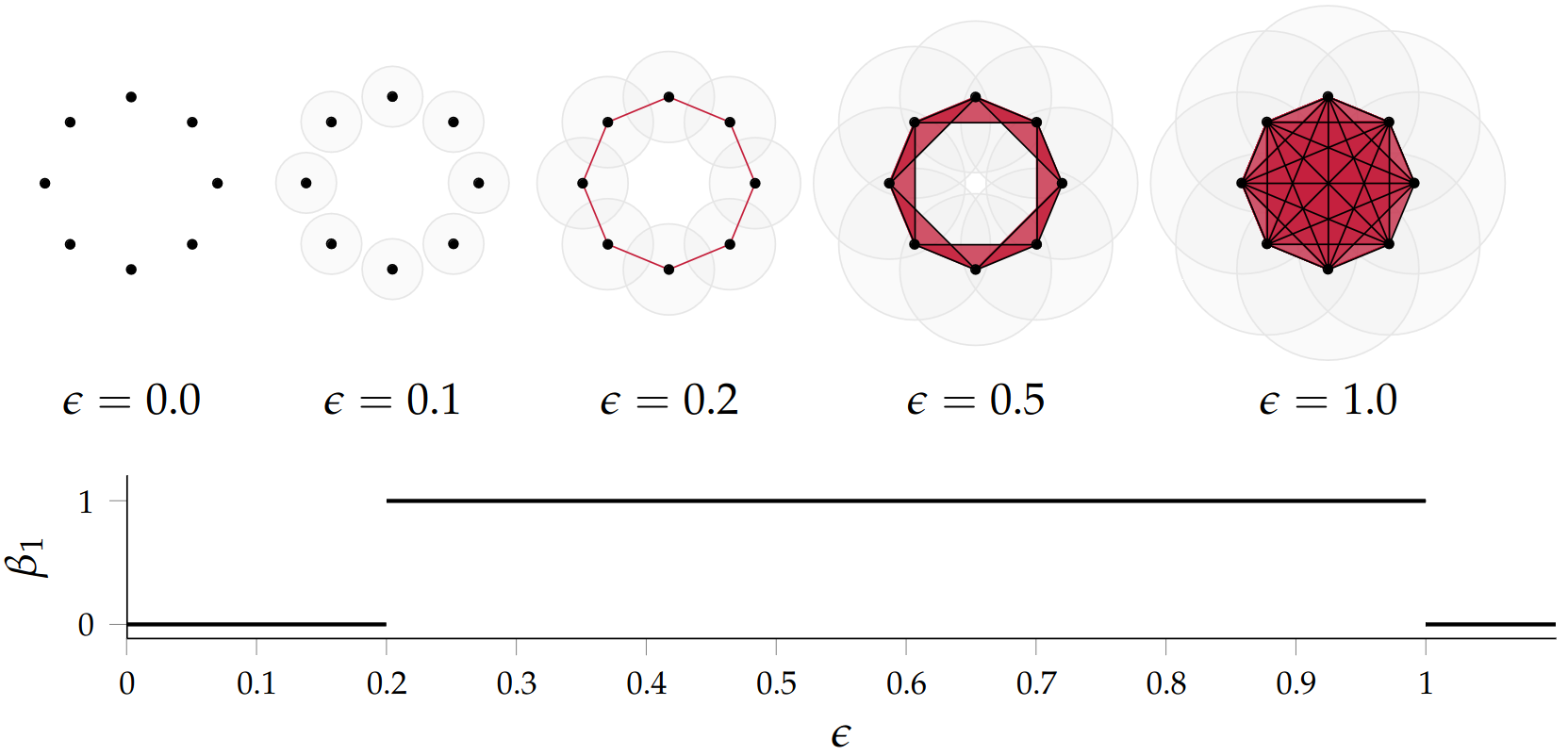
Slides based on Bastian Rieck’s Topological Data Analysis for Machine Learning
Issues with this approach
How to pick \(\epsilon\)?
There might not be one ‘correct’ value for \(\epsilon\).
Computationally inefficient
Slides based on Bastian Rieck’s Topological Data Analysis for Machine Learning
Picking \(\epsilon\) - Topological Persistence
Intuition: Go through all scales and track the topological features

Slides based on Bastian Rieck’s Topological Data Analysis for Machine Learning
Picking \(\epsilon\) - Topological Persistence
Intuition: Go through all scales and track the topological features

Slides based on Bastian Rieck’s Topological Data Analysis for Machine Learning
Picking \(\epsilon\) - Topological Persistence
Intuition: Go through all scales and track the topological features

Slides based on Bastian Rieck’s Topological Data Analysis for Machine Learning
Picking \(\epsilon\) - Topological Persistence
Intuition: Go through all scales and track the topological features

Slides based on Bastian Rieck’s Topological Data Analysis for Machine Learning
Picking \(\epsilon\) - Topological Persistence
Intuition: Go through all scales and track the topological features

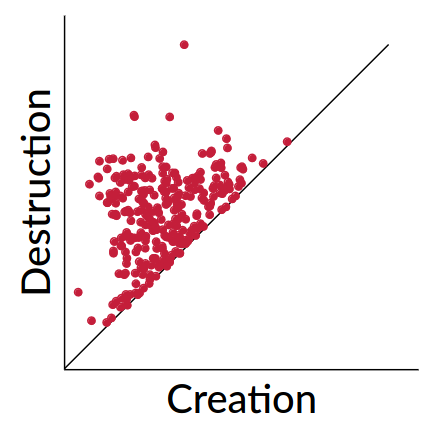
Slides based on Bastian Rieck’s Topological Data Analysis for Machine Learning
Strategy 2: Data skeleton
The Mapper Algortihm
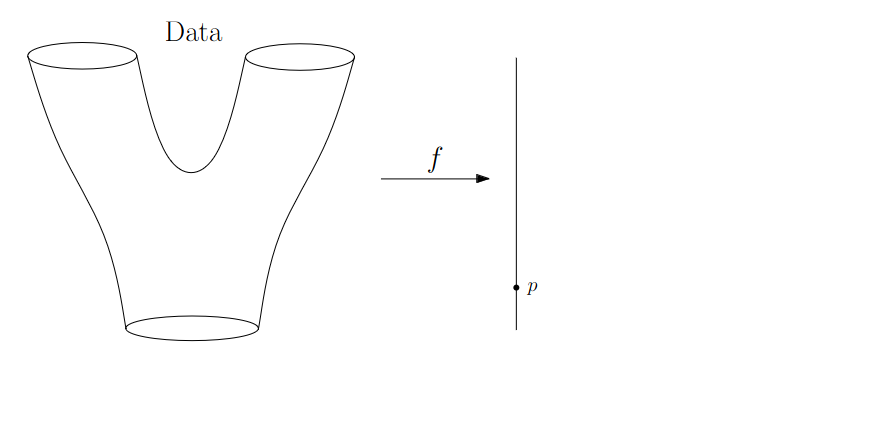
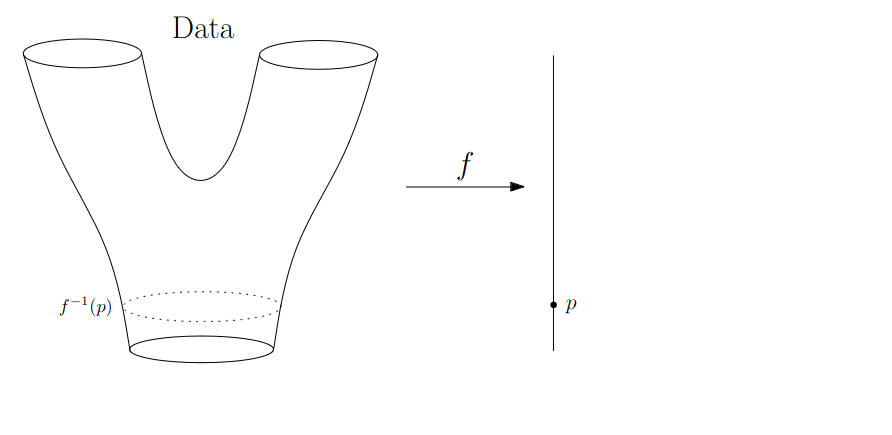
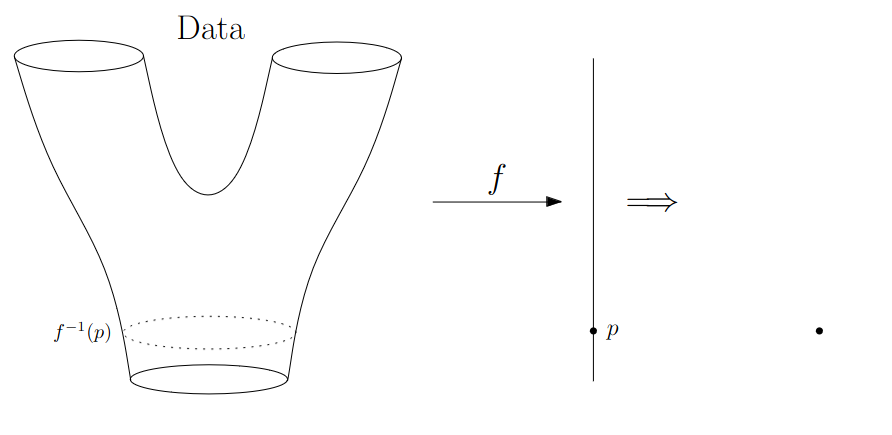
Math World
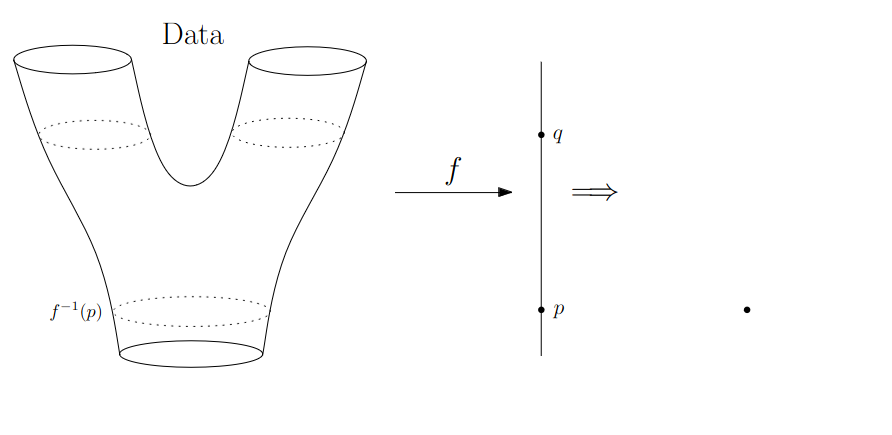
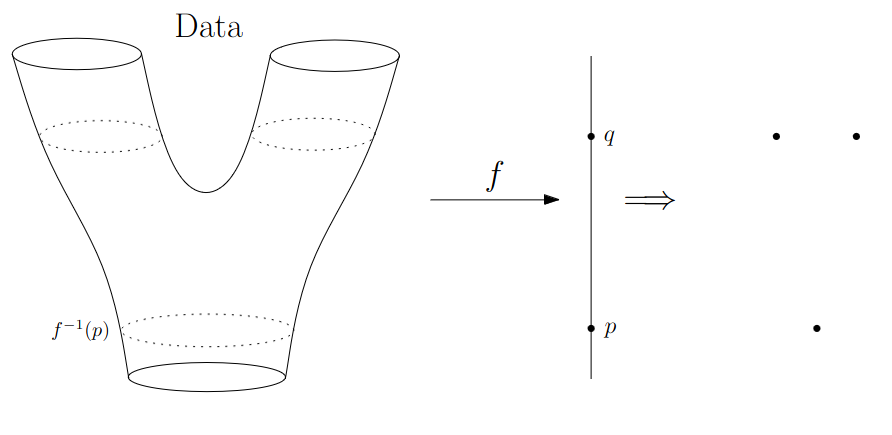
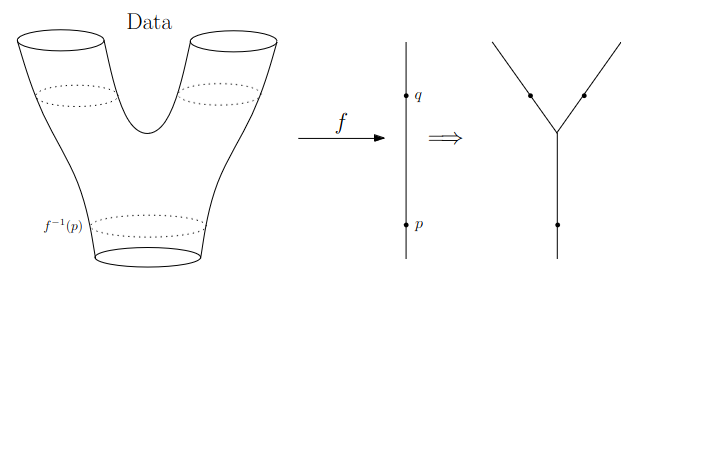
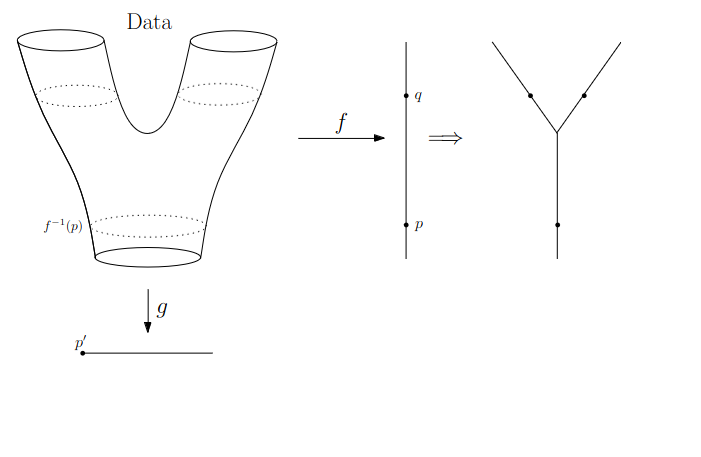
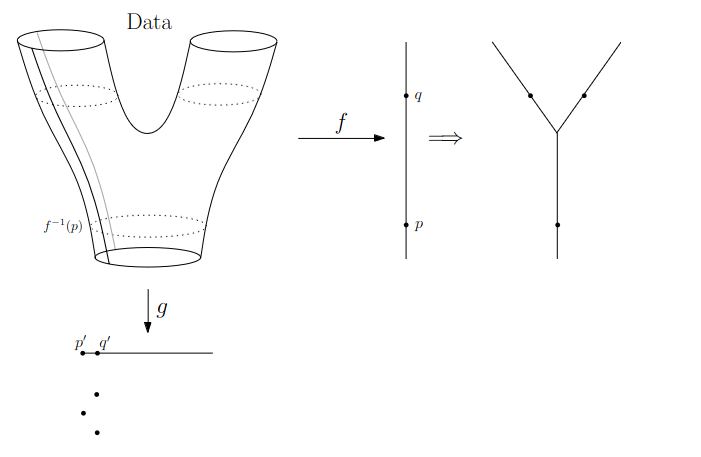
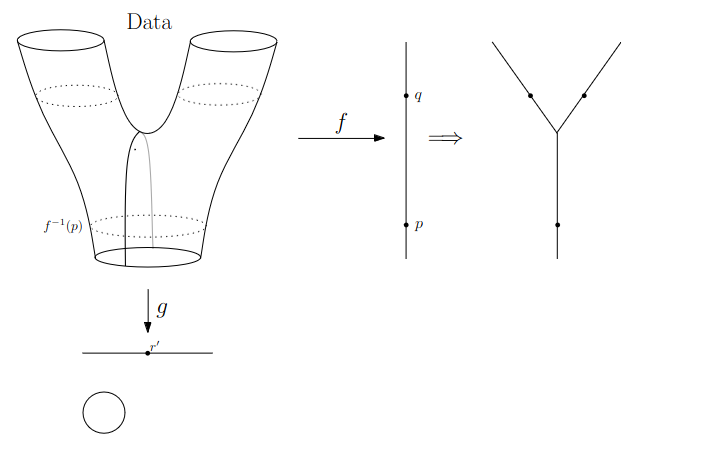
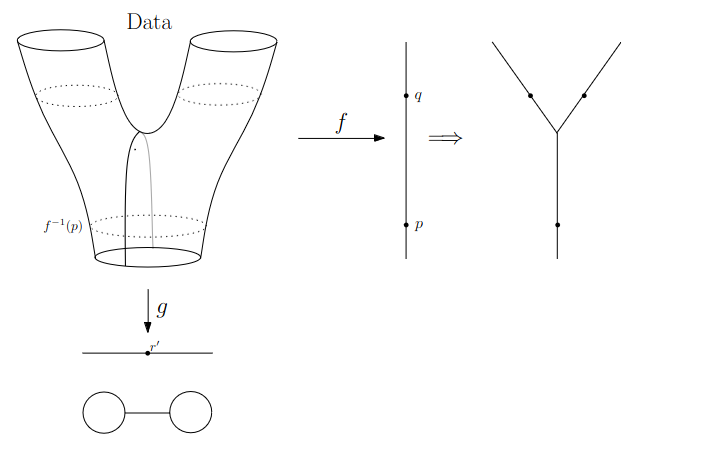
We start in “Math World”, where
- We draw the data as a smooth manifold
- Functions that appear are smooth or continuous
We will not need either of these assumptions once we are in the “Data World”.
Even more importantly, data in the real world is never like this.
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Math World

Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Math World
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Math World
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Math World
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Math World
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Math World
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Math World
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Math World
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Math World
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Math World
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Math World

Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Math World
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Math World
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Math World
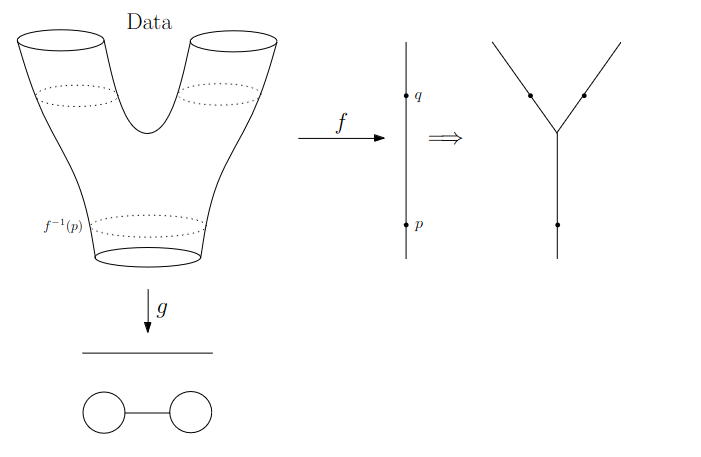
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Why is this useful?
We get “easy” understanding of the localizations of quantities of interest.
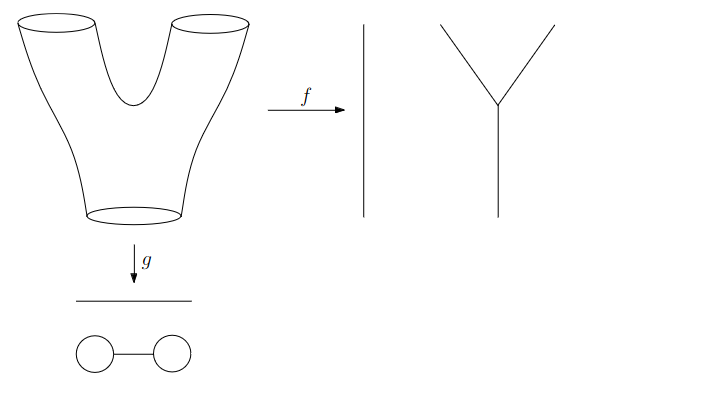
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Why is this useful?
We get “easy” understanding of the localizations of quantities of interest.

Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Why is this useful?
We get “easy” understanding of the localizations of quantities of interest.
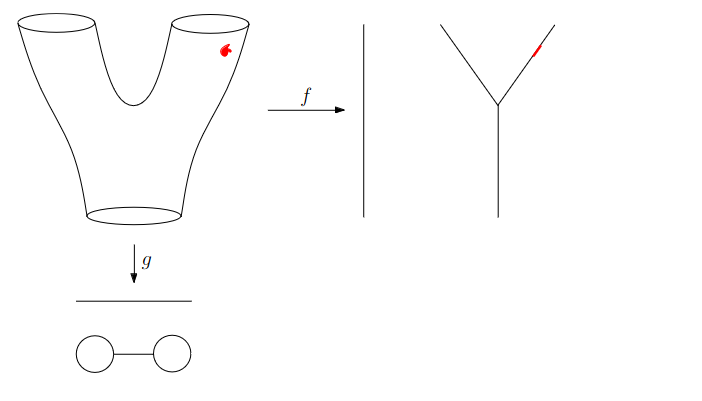
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Why is this useful?
We get “easy” understanding of the localizations of quantities of interest.
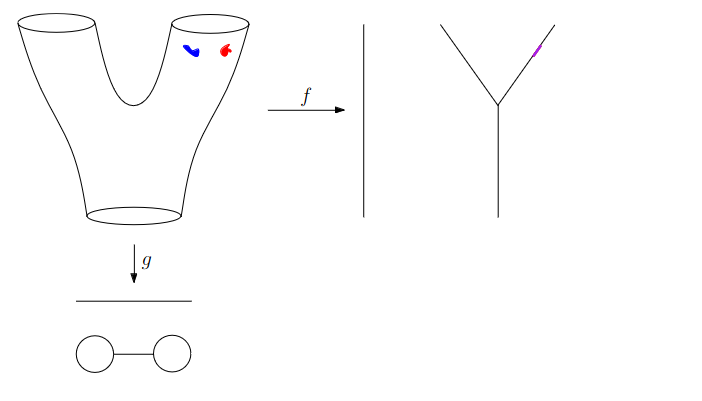
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Why is this useful?
We get “easy” understanding of the localizations of quantities of interest.
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Why is this useful?
We get “easy” understanding of the localizations of quantities of interest.
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Why is this useful?
We get “easy” understanding of the localizations of quantities of interest.
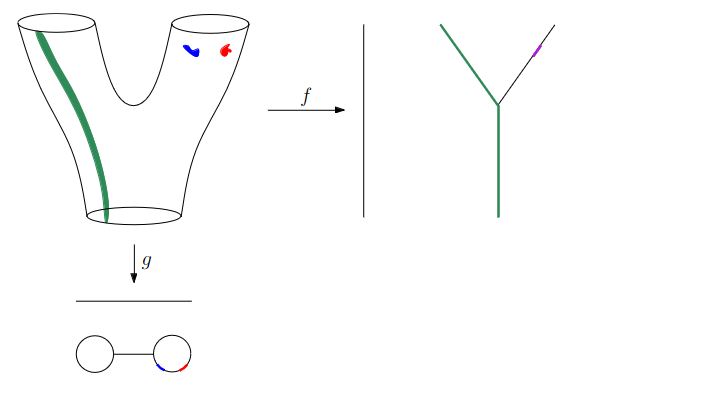
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Why is this useful?
We get “easy” understanding of the localizations of quantities of interest.
- Lenses inform us where in the space to look for phenomena.
- For easy localizations many different lenses will be informative.
- For hard (= geometrically distributed) localizations we have to be more careful. But even then, we frequently get incremental knowledge from a poorly chosen lens.
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
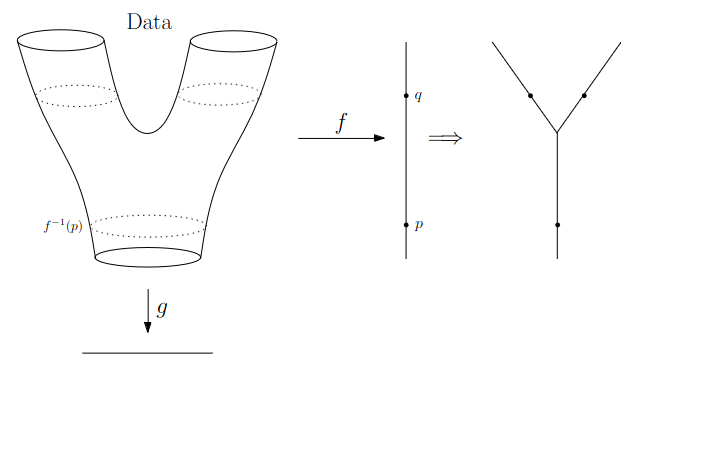
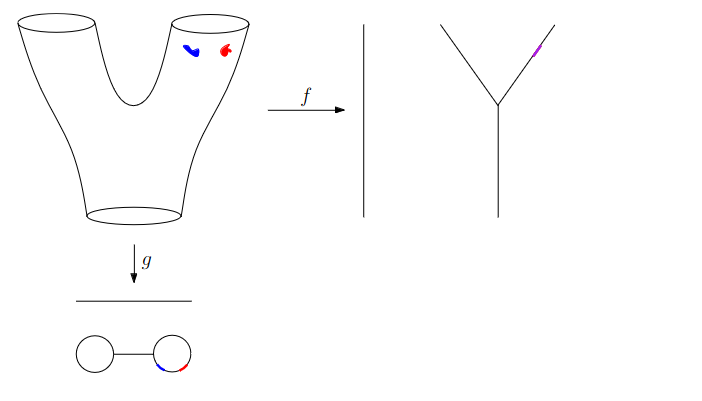
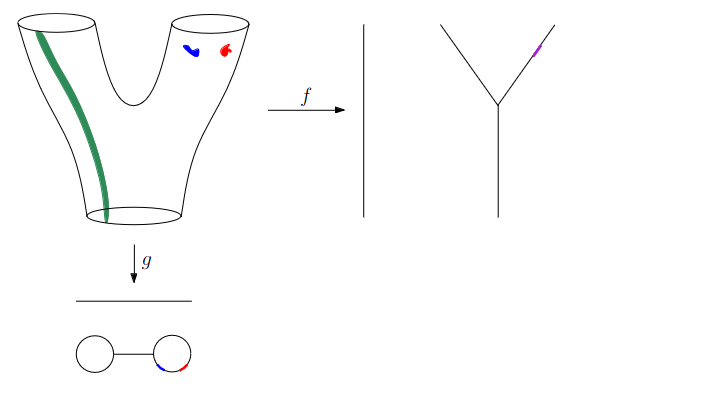
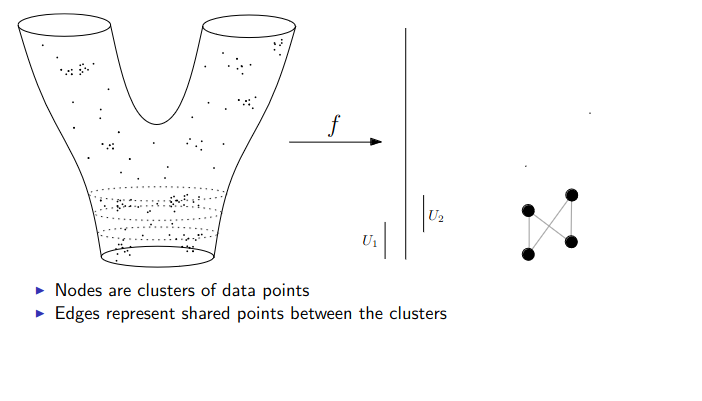
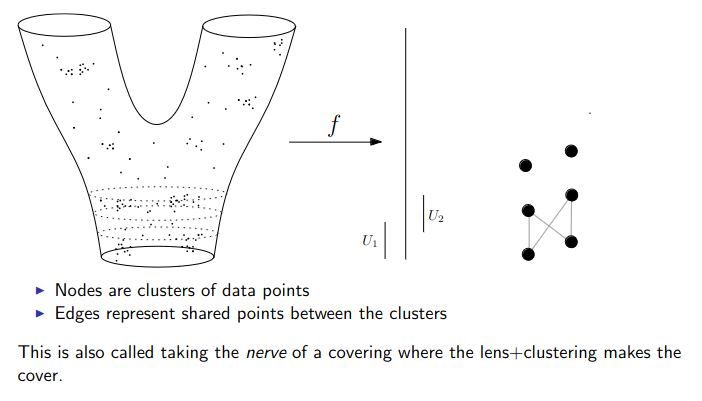
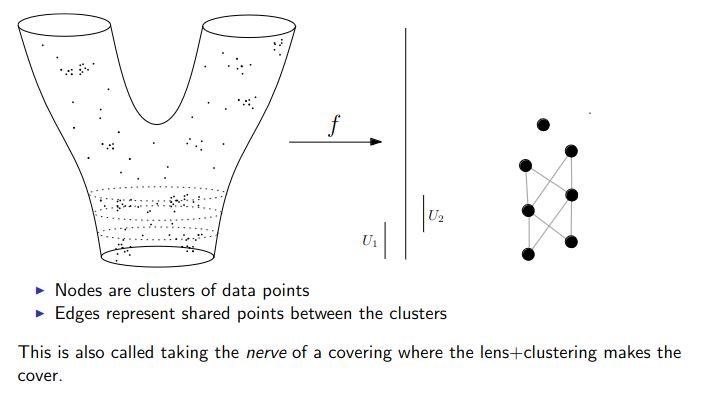
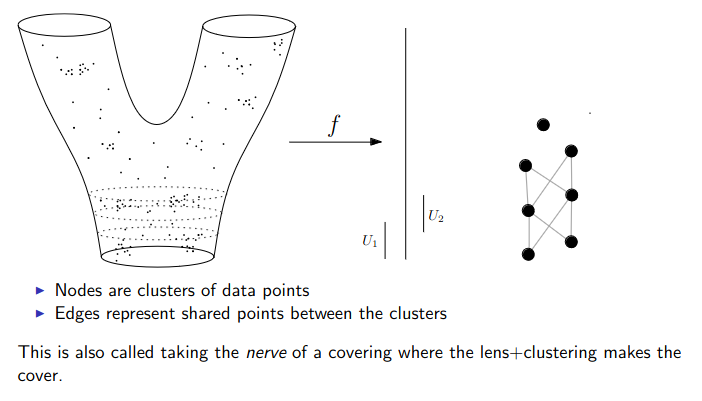
Data World - Mapper
We need to adjust the “Math World” view to bring the algorithm into the “Data World”
- We replace points with open sets in the range of the lens
- We replace “connected component of the inverse image” with “clusters in the inverse image”
- We connect clusters (nodes) with an edge if they share points in common.
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Data World - Mapper
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Data World - Mapper
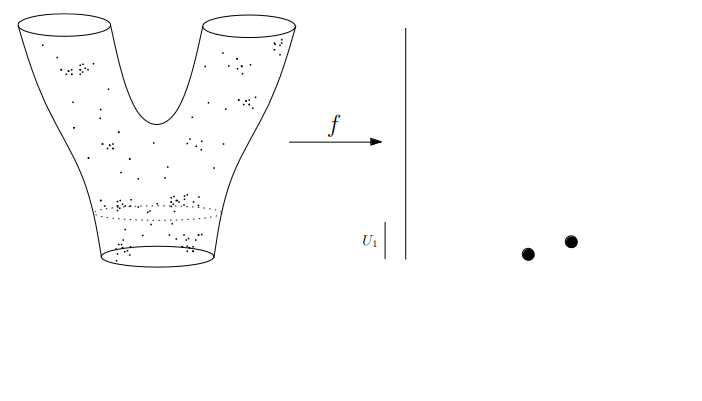
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Data World - Mapper
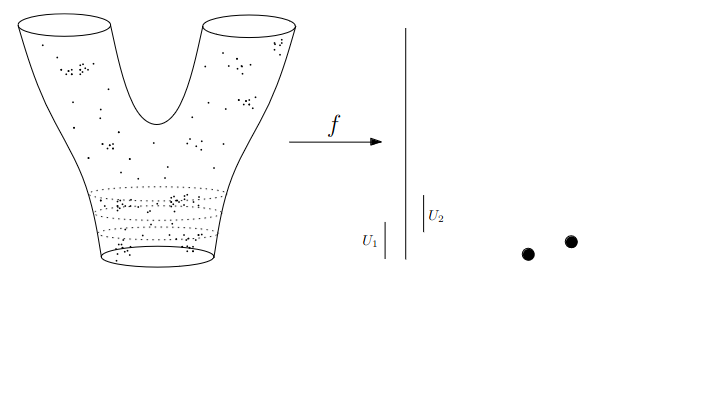
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Data World - Mapper
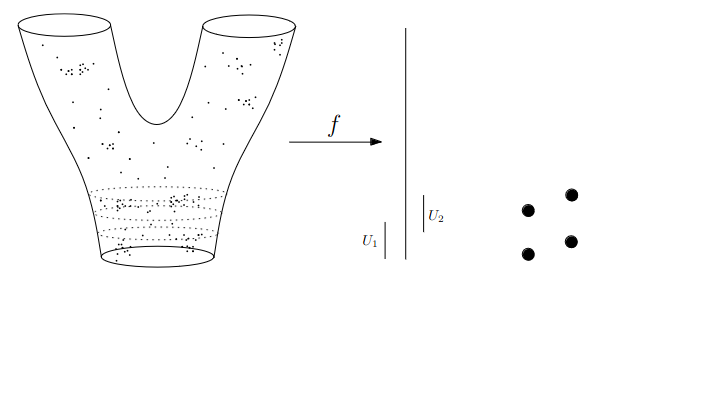
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Data World - Mapper
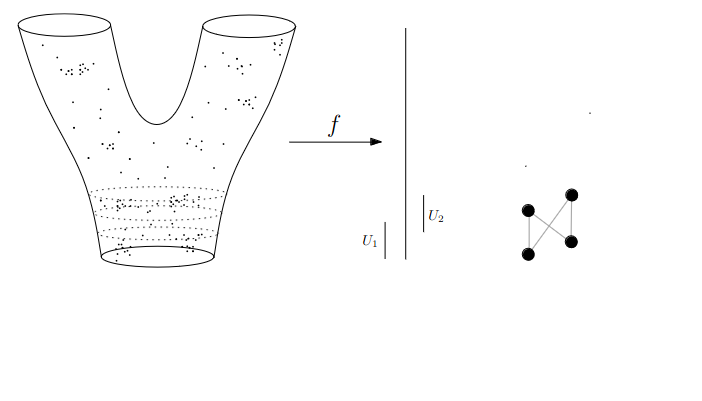
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Data World - Mapper
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Data World - Mapper
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Data World - Mapper

Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Data World - Mapper
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Data World - Mapper
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Data World - Mapper

Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Data World - Mapper
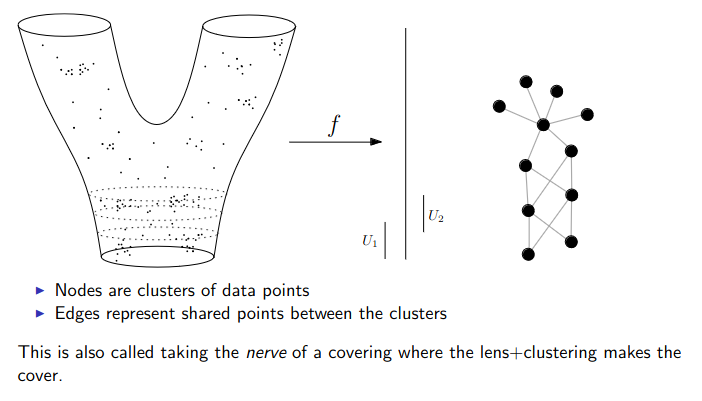
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
Data World - Mapper
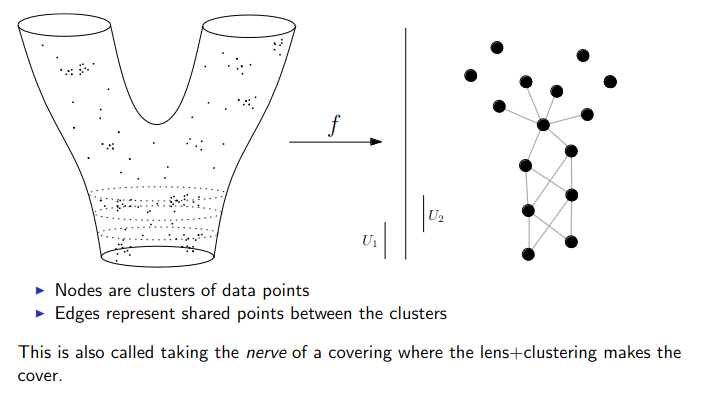
Slides based on Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
To look further
References
For more information about the persistence diagram, see Vincent Divol’s CDS Lunch Seminar presentation “Quantifying the topology of datasets using Topological Data Analysis”
For more information about the mapper algorithm, see Anthony Bak’s Stanford Seminar - Topological Data Analysis presentation
To learn more about TDA for Machine Learning, see Bastian Rieck’s Topological Data Analysis for Machine Learning tutorial (around 4 hours total)
For a course in TDA, see Raphaël Tinarrage’s Topological Data Analysis with Persistent Homology summer course
References
Some books of interest:
Edelsbrunner, Herbert, and John L. Harer. Computational topology: an introduction. American Mathematical Society, 2022.
Dey, Tamal Krishna, and Yusu Wang. Computational topology for data analysis. Cambridge University Press, 2022.
Carlsson, Gunnar, and Mikael Vejdemo-Johansson. Topological data analysis with applications. Cambridge University Press, 2021.
Introductory paper:
- Chazal, Frédéric, and Bertrand Michel. “An introduction to topological data analysis: fundamental and practical aspects for data scientists.” Frontiers in artificial intelligence 4 (2021): 108.
References
TDA in Python:
- For overall TDA data structures and algorithms: GUDHI (both C++ and Python) or scikit-tda
- For a faster implementation of the Vietoris-Rips: Ripser.py
- For a faster implementation of the Mapper: KeplerMapper
For an open-source library and software collection for topological data analysis and visualization: Topology ToolKit
For more examples of TDA aplications:
- DONUT - Database of Original & Non-Theoretical Uses of Topology
- Applied Algebraic Topology Research Network seminar series
