Visualization for Machine Learning
## Today’s Class - Model Interpretation and Explanation - White-box Approaches and Visualizations - Related Research in VIS & AI ## Today’s Class - Model Interpretation and Explanation - White-box Approaches and Visualizations - Related Research in VIS & AI ## Why Model Interpretation & Explanation? ::: {.columns} ::: {.column width="50%"}  ::: ::: {.column width="50%"} - Model Validation and Improvement - Decision Making and Knowledge Discovery - Gain Confidence and Obtain Trust ::: ::: ## Machine-learning-assisted materials discovery using failed experiments ::: {.columns} ::: {.column width="40%"} 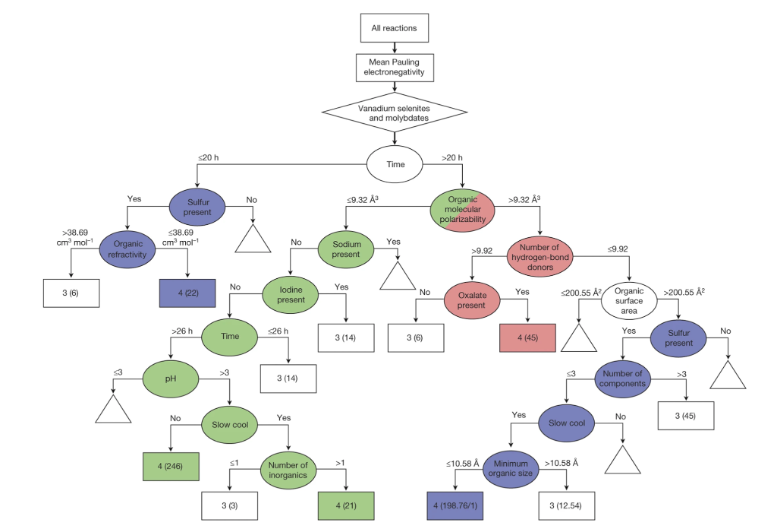 ::: ::: {.column width="60%"} - Researchers firstly built a database of chemistry experiments (new material). - Then they train an SVM to predict whether a new chemistry experiment will be successful. - Then they train a surrogate DT to explain the model to learn more about the experiment. ::: ::: ## Why Model Interpretation & Explanation? ::: {.columns} ::: {.column width="40%"}  ::: ::: {.column width="60%"} - Fairness - Privacy - Reliability or Robustness - Causality - Trust ::: ::: ## How Do We Interpret Model Behavior? Methods for machine learning model interpretation can be classified according to various criteria. - **White-box / Intrinsic interpretability**: Machine learning models that are considered interpretable due to their simple structure, such as short decision trees or sparse linear models. Interpretability is gained by explaining the internal structure of the model. - **Black-box / Post-hoc interpretability**: Machine learning models that are hard to gain a comprehensive understanding of their inner working (e.g., deep neural networks) are considered black boxes. Interpretability is gained by explaining the model behavior after training. [Taxonomy of Interpretability Methods](https://christophm.github.io/interpretable-ml-book/taxonomy-of-interpretability-methods.html) ## Today’s Class - Model Interpretation and Explanation - White-box Approaches and Visualizations - Related Research in VIS & AI ## White-box Models We discuss the following models that are intrinsically interpretable: - Linear Regression - Generalized Additive Models (GAM) - Tree-based Models - Decision Rules ## Linear Regression Linear models can be used to model the dependence of a regression target y on some features x in a format as below: \begin{equation} y = \beta_0 + \beta_1 x_1 + \ldots + \beta_n x_n + \varepsilon\end{equation} The predicted target $y$ is a linear combination of the weighted features $\beta_i x_i$. The estimated linear equation is a hyperplane in the feature/target space (a simple line in the case of a single feature). The weights specify the slope (gradient) of the hyperplane in each direction. ## Linear Regression 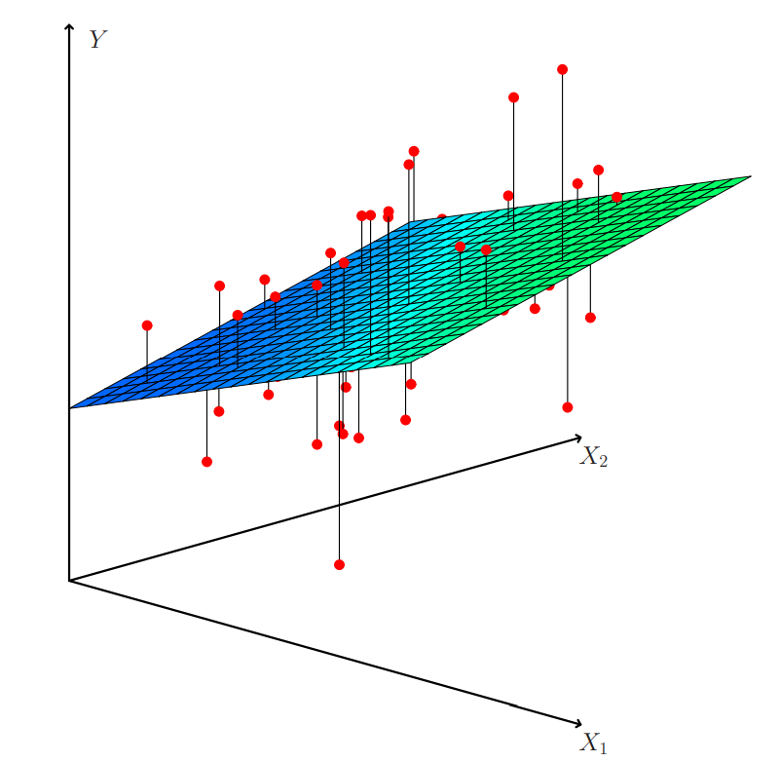 ## Linear Regression: An Example of Housing Price 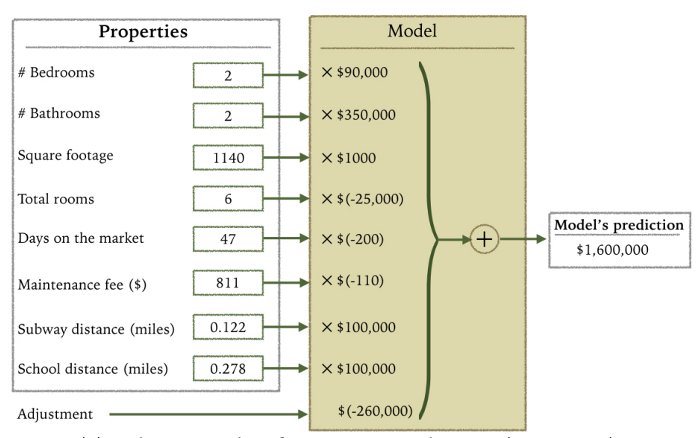 How do you interpret the influence of each property on the prediction of housing price? ## Evaluation of Linear Regression Model ### R Square $R^2$ (R-squared) \begin{equation} R^2 = 1 - \frac{\sum (y_i - \hat{y}_i)^2}{\sum (y_i - \bar{y})^2} \end{equation} Mean Square Error (MSE)/Root Mean Square Error (RMSE) \begin{equation} MSE = \frac{1}{N} \sum_{i=1}^{N} (y_i - \hat{y}_i)^2 \end{equation} Mean Absolute Error (MAE) \begin{equation} MAE = \frac{1}{N} \sum_{i=1}^{N} |y_i - \hat{y}_i| \end{equation} ## Visual Analytics (VA) Systems for Linear Regression ::: {.columns} ::: {.column width="40%"}  ::: ::: {.column width="60%"} There is a trade-off between model complexity (number of features) and accuracy. This VA system helps model building (feature ranking) and model validation. ::: ::: ## Pros and Cons of Linear Models ::: {.columns} ::: {.column width="50%"} Pros: ::: ::: {.column width="50%"} Cons: ::: ::: ## Pros and Cons of Linear Models ::: {.columns} ::: {.column width="50%"} Pros: Easily interpretable Statistical guarantees on inference (if assumptions are satisfied) No hyperparameters (analytical solution) ::: ::: {.column width="50%"} Cons: $X$’s relationship with $Y$ can be non-linear. In these cases, linear regression may not provide good results. If you don’t satisfy certain assumptions (namely normal distribution of residuals and homoscedasticity), then inference can be incorrect. ::: ::: ## Limitations of Linear Models - Features are assumed to follow Gaussian distribution - No interactions between features What if your dataset does not follow the assumptions? ## Generalized Additive Models (GAMs) Generalized additive models extend standard linear models by allowing non-linear functions of each of the variables. \begin{equation} y_i = \beta_0 + \sum_{j=1}^{p} f_j(x_{ij}) + \varepsilon_i \\ = \beta_0 + f_1(x_{i1}) + f_2(x_{i2}) + \dots + f_p(x_{ip}) + \varepsilon_i \end{equation} ## Generalized Additive Models (GAMs): An Example \begin{equation} Wage = f(year, age, education) = b_0 + f_1(year) + f_2(age) + f_3(education) \end{equation} 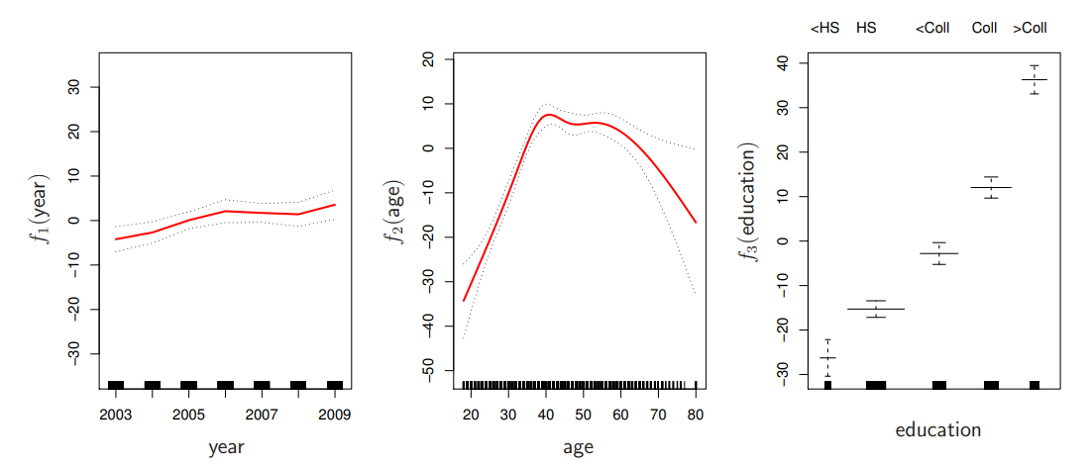 ## Training GAMs (Backfitting) 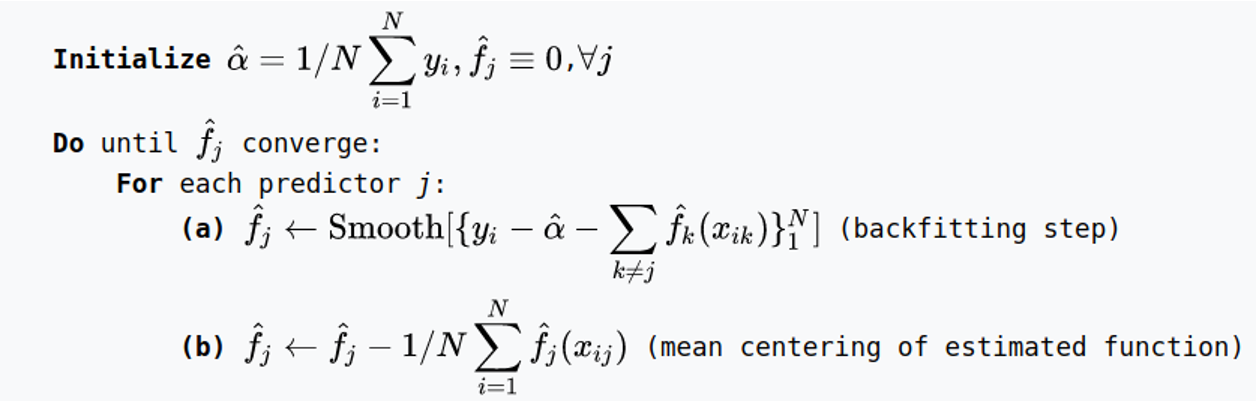 ## Generalized Additive Models (GAMs): Pros and Cons ::: {.columns} ::: {.column width="50%"} Pros: GAMs allow us to fit a non-linear $f_j$ to each $X_j$ , so that we can model non-linear relationships easily. The non-linear fits can potentially lead to better predictions. Because the model is additive, we can examine the effect of each $X_j$ on $Y$ for each observation. This is useful for visualization. ::: ::: {.column width="50%"} Cons: GAMs are restricted to be additive. With many variables, important interactions can be missed or computationally infeasible to find. ::: ::: ## Explainable Boosting Machines ::: {.columns} ::: {.column width="65%"} \begin{equation} g(\mathbb{E}[y]) = \beta_0 + \sum f_j(x_j) \end{equation} \begin{equation} g(\mathbb{E}[y]) = \beta_0 + \sum f_j(x_j) + \sum f_{ij}(x_i, x_j) \end{equation} ::: ::: {.column width="35%"} However, as with linear regression, we can manually add interaction terms to the GAM model by including additional predictors of the form $X_j \times X_k$. In addition we can add low-dimensional interaction functions of the form $f_{jk}(X_j , X_k)$ into the model. ::: ::: ## Explainable Boosting Machines ::: {.columns} ::: {.column width="65%"} \begin{equation} g(\mathbb{E}[y]) = \beta_0 + \sum f_j(x_j) \end{equation} \begin{equation} g(\mathbb{E}[y]) = \beta_0 + \sum f_j(x_j) + \sum f_{ij}(x_i, x_j) \end{equation} ::: ::: {.column width="35%"} What if we have a lot of interactions? How do we choose our interactions? ::: ::: ## Explainable Boosting Machines ## Visualizing EBMs (or GAMs) 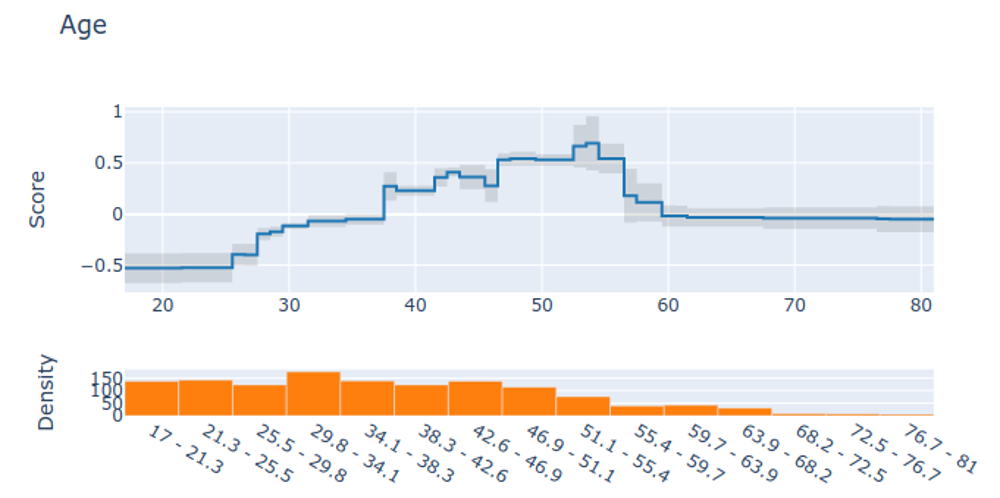 ## Visualizing EBMs (or GAMs) 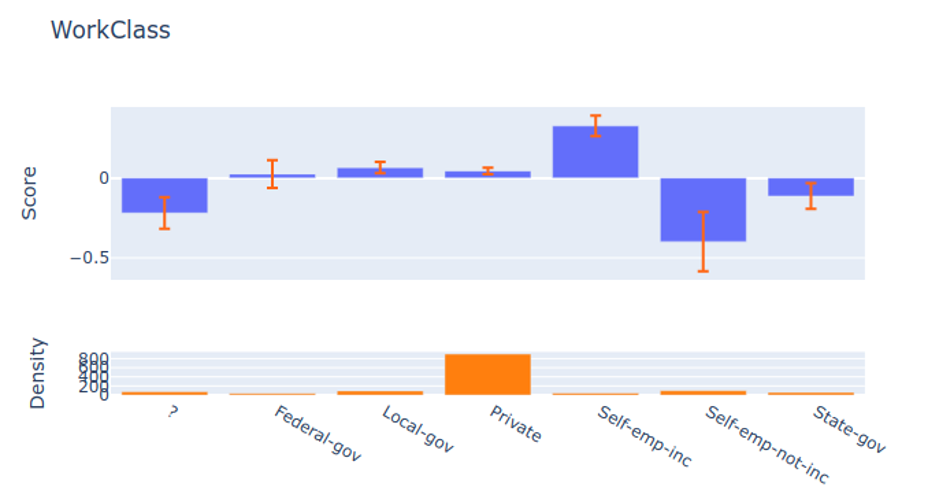 ## Visualizing EBMs (or GAMs) 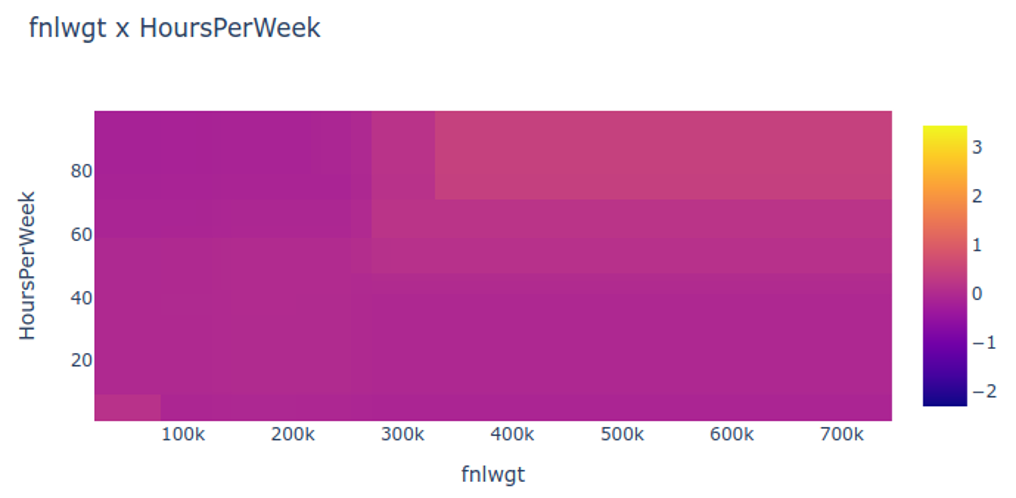 ## Visualizing EBMs (or GAMs) 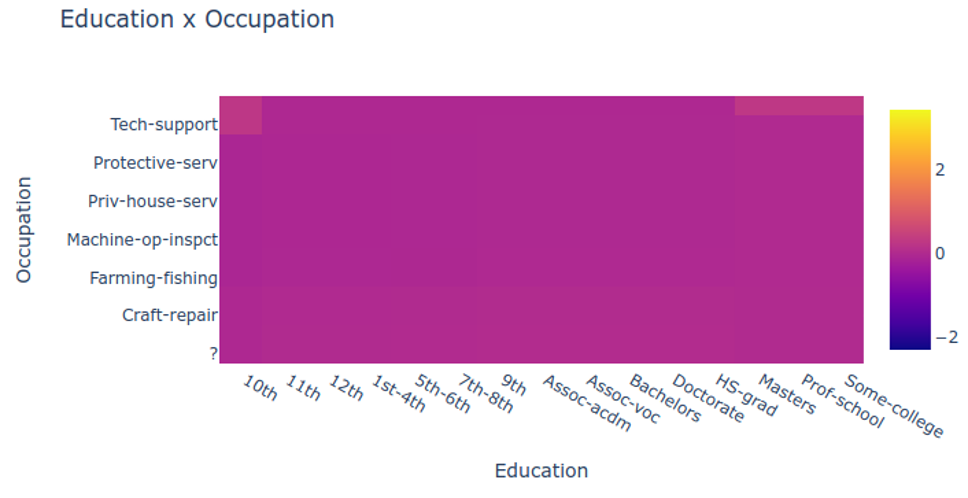 ## Visual Analytics (VA) Systems Using GAMs ](./figures/paper5.png) ## Visual Analytics (VA) Systems Using GAMs  ## Visual Analytics (VA) Systems Using GAMs 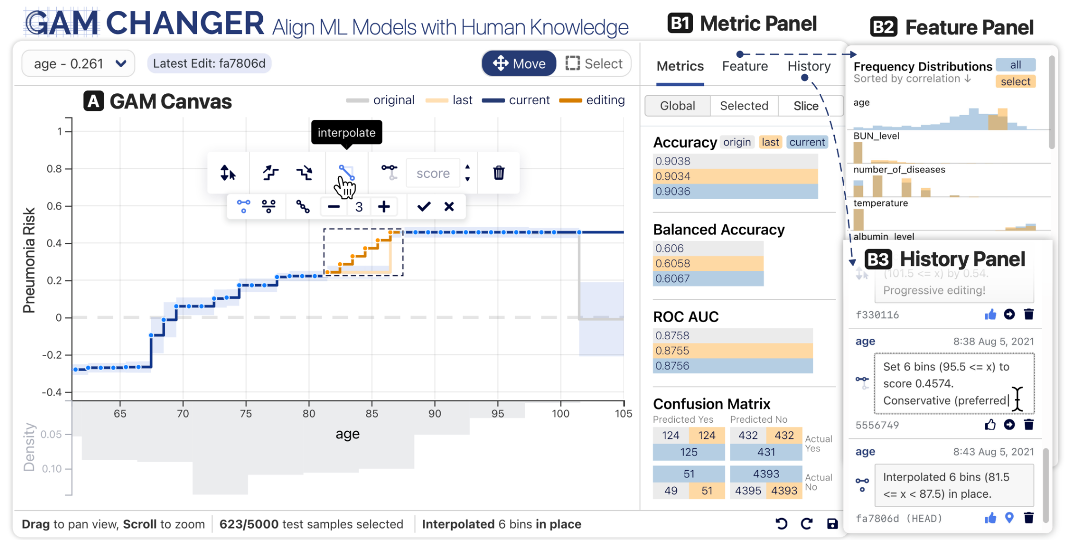 https://arxiv.org/pdf/2112.03245.pdf https://github.com/interpretml/gam-changer ## Practice 1 Notebook: https://colab.research.google.com/drive/1nKE6WIApebHi67yfhH6k5mZN86evLZOM?usp=sharing Some other libraries for PDP visualization: https://scikit-learn.org/stable/modules/partial_dependence.html https://interpret.ml/docs/pdp.html ## BREAK ## Tree-based Models: Example 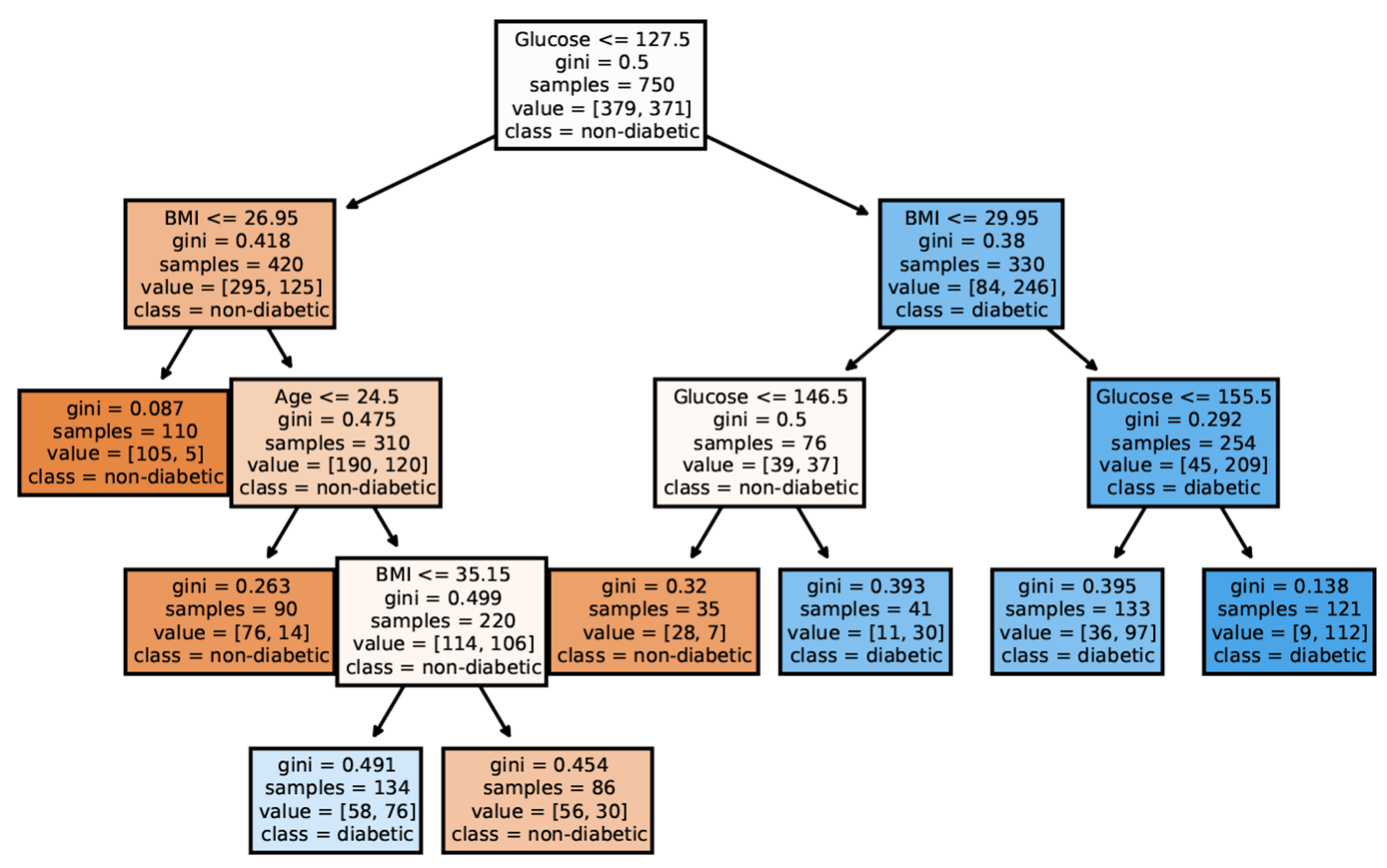 ## Visualization of Trees https://treevis.net/ provides a gallery of tree visualization. These trees are used to visualize hierarchical structures, but not just tree-based machine learning models.  ## VA Systems Using Tree-based Models ::: {.columns} ::: {.column width="65%"} 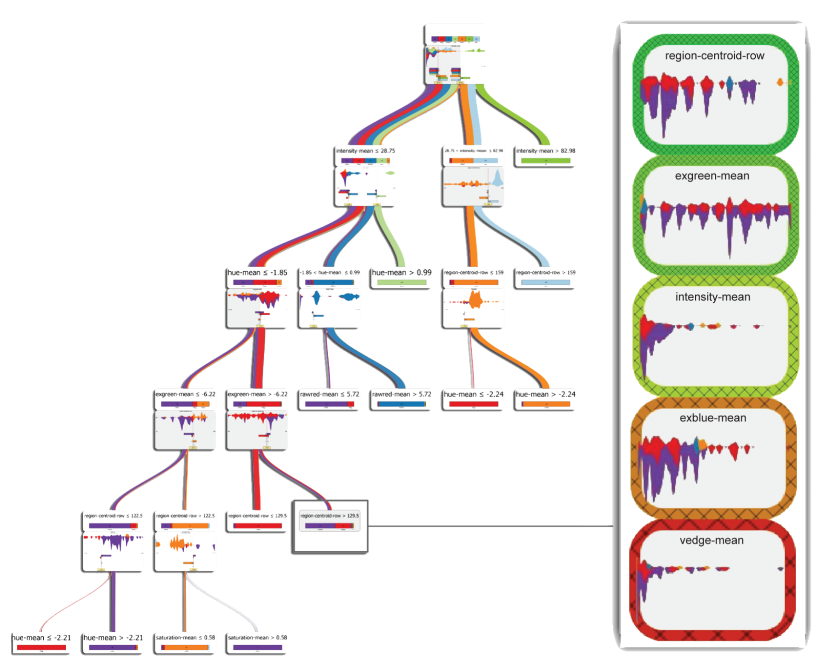 ::: ::: {.column width="35%"} It shows the flow of different class, and the class distribution in along the feature values. ::: ::: ## VA Systems Using Tree-based Models 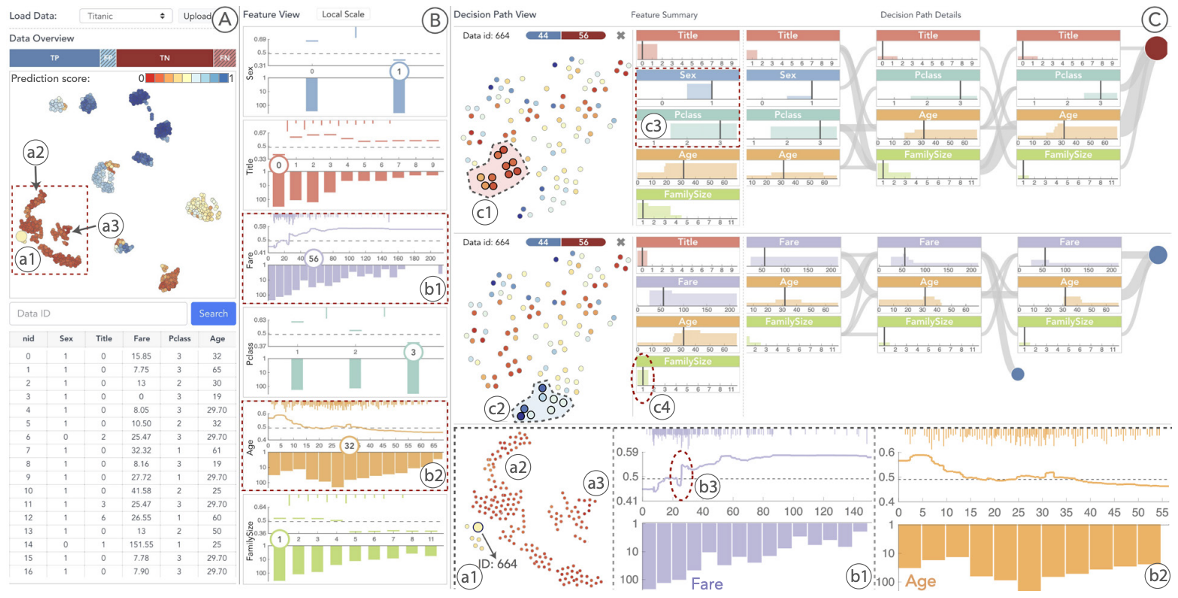 ## Decision Rules: Different Structures ::: {.columns} ::: {.column width="50%"}  Clearly see how the decision is made and which rule is more important. ::: ::: {.column width="50%"}  The final decision is made based on a voting mechanism. A recent user study shows that “if-then structure without any connecting else statements enables users to easily reason about the decision boundaries of classes.” ::: ::: ## Decision Rules: Different Structures Disjunctive normal form (DNF, OR-of-ANDs) Conjunctive normal form (CNF, AND-of-ORs)  ## Decision Rules: Visual Factors Influence Rule Understanding ::: {.columns} ::: {.column width="65%"} 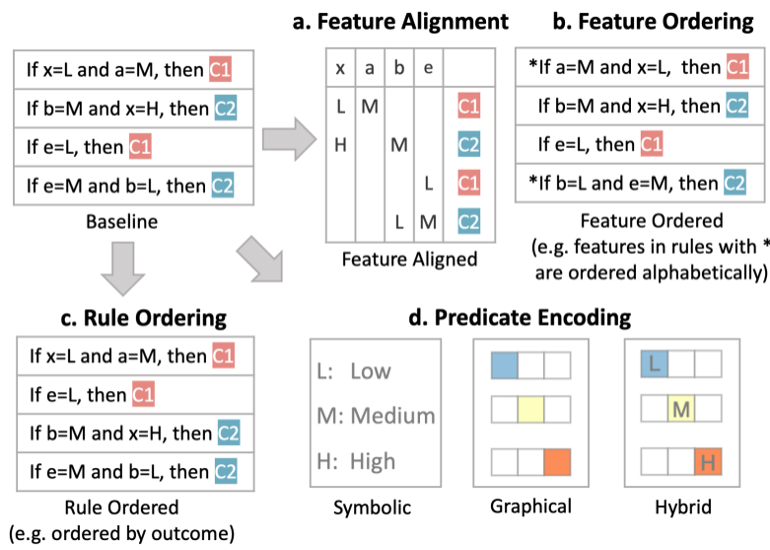 ::: ::: {.column width="35%"} Can different visualizations of rules lead to different level of understanding of rules? If so, what are the visual factors influence understanding and how they play a role in rule understanding? ::: ::: ## Evaluation of Rules Given a rule below: If $X$, then class $Y$. Support / Coverage of a rule: \begin{equation} \text{Support} = \frac{\text{number of instances that match the conditions in } X}{\text{total number of instances}} \end{equation} Confidence / Accuracy of a rule: \begin{equation} \text{Confidence} = \frac{\text{number of instances that match conditions in } X \text{ and belong to class } Y}{\text{number of instances that match conditions in } X} \end{equation} ## Global Surrogate Imagine that we have a black-box model (too complex to understand the internal structure), can we use white-box models to help us understand the model behavior of the black-box model?  ## Global Surrogate Open the black box by understanding a “surrogate model” that approximate the behavior of the original black-box model. 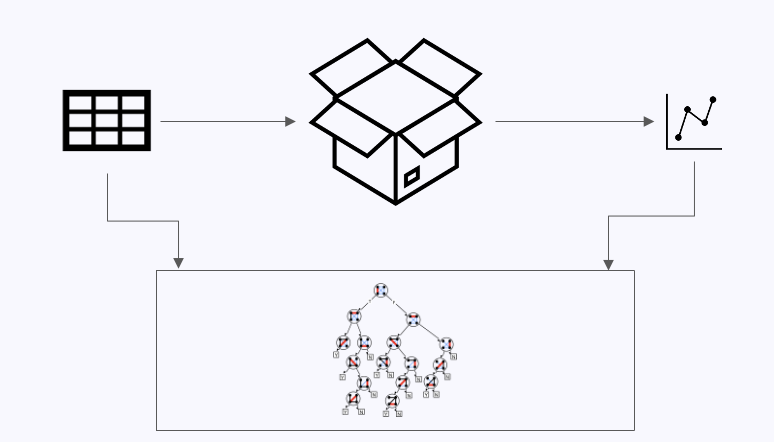 ## However… What you want: 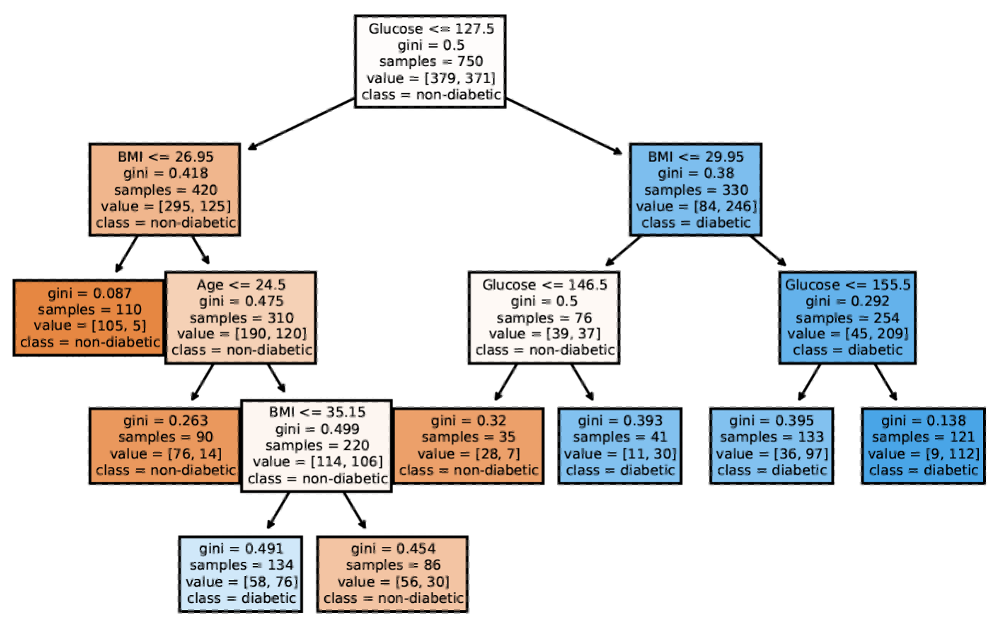{width=540px} What you get:  ## VA System for Rule List 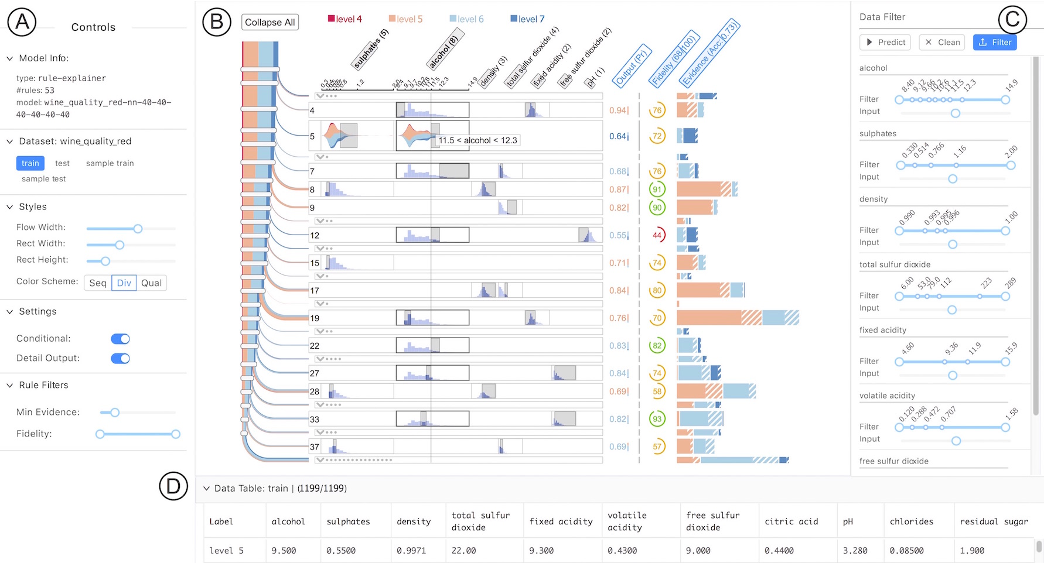 ## VA Systems for Rules in Random Forest 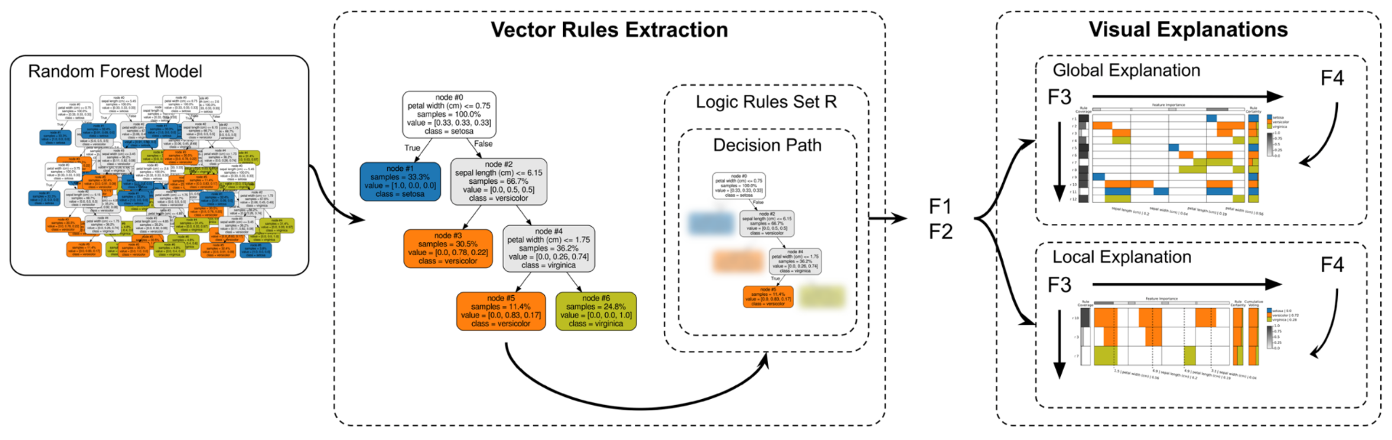 ## Other white-box models? - Naive Bayes - K-nearest neighbors - etc. ## Practice 2 Notebook: https://colab.research.google.com/drive/12LV2Z_1BbP3efACYp2QxzsPaOrIn8a8l?usp=sharing ## Today’s Class - Model Interpretation and Explanation - White-box Approaches and Visualizations - Related Research in VIS & AI ## Manipulating and Measuring Model Interpretability 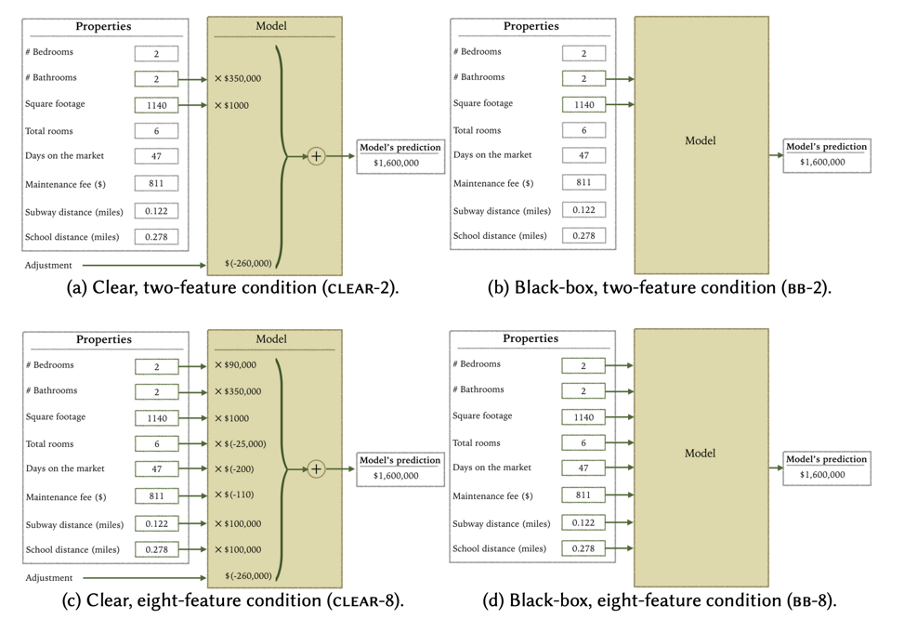 https://arxiv.org/abs/1802.07810 ## Stop explaining black box machine learning models for high stakes decisions  https://www.nature.com/articles/s42256-019-0048-x ## Slice Finder: Automated Data Slicing for Model Validation ::: {.columns} ::: {.column width="50%"}  ::: :::{.column width="50%"} How about we use whether the model prediction is wrong or not to train a “surrogate tree”? ::: ::: https://ieeexplore.ieee.org/stamp/stamp.jsp?tp=&arnumber=8731353 ## Toolkits InterpretML: https://github.com/interpretml/interpret